探究OpenGL中法向变换
学习LearnOpenGL教程的过程中,光照模型章节讲到对于法向的变换与顶点的变换不同,有一个专门的法向矩阵来计算,本文参考The Normal Matrix和个人理解将法相矩阵的计算过程整理如下。
法向和顶点变换的区别
法向和顶点的不同在于,顶点使用三维坐标的形式来表示一个位置,而法向则是用三维坐标表示一个方向。如果对顶点进行了不等比的变换,这种变换如果作用在法向上,就会导致法向不会再垂直与对应的表面了,自然光照的计算就变得不准确了。下图,说明了这种现象:

正确计算法向的变换
法向有一个特性,不论在变换前还是变换后都应该保证:法向垂直于对应的面。根据此特性,我们可以对法向的变换矩阵进行推导。
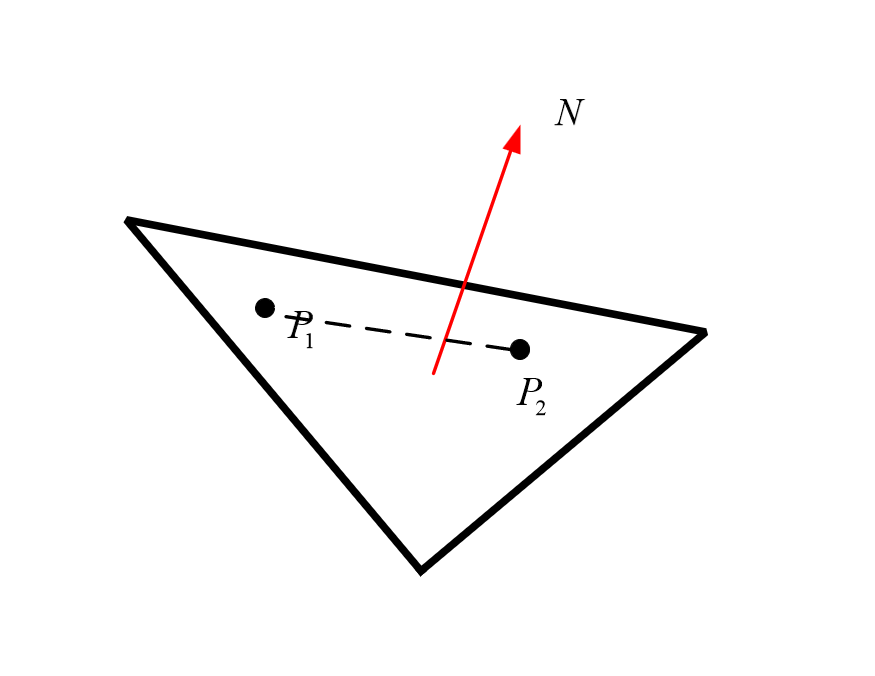
如上图所示,一个三角面其法向为N,那么对其面上的任意两个顶点P1和P2都有法向垂直与向量P1P2,即:
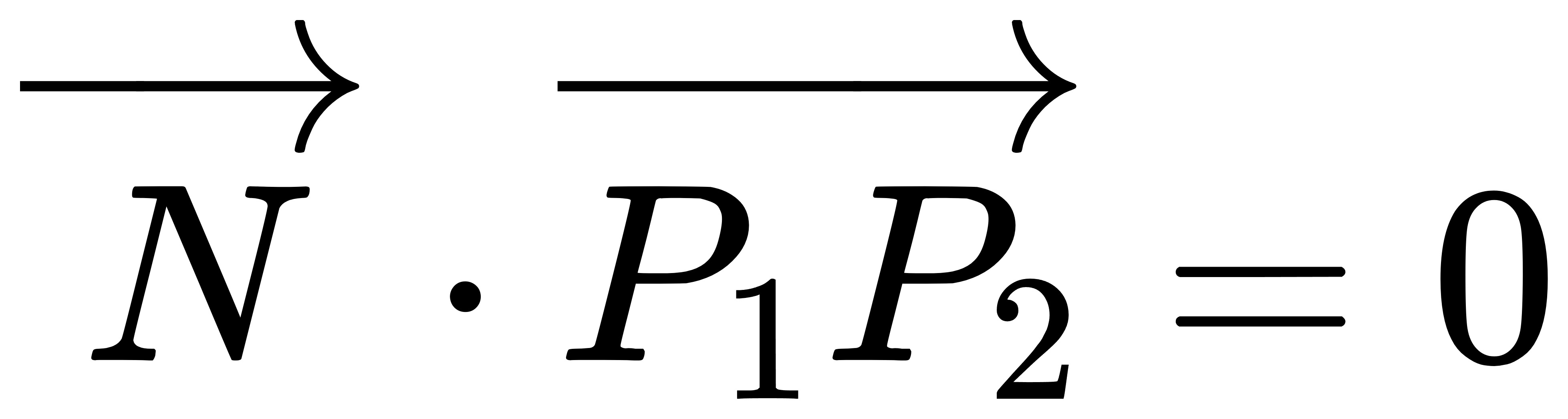
如果使用矩阵表示上述垂直关系,记N表示法向量,T表示向量P1P2,则可以表示为(这里向量统一为列向量,因此N需要转置):
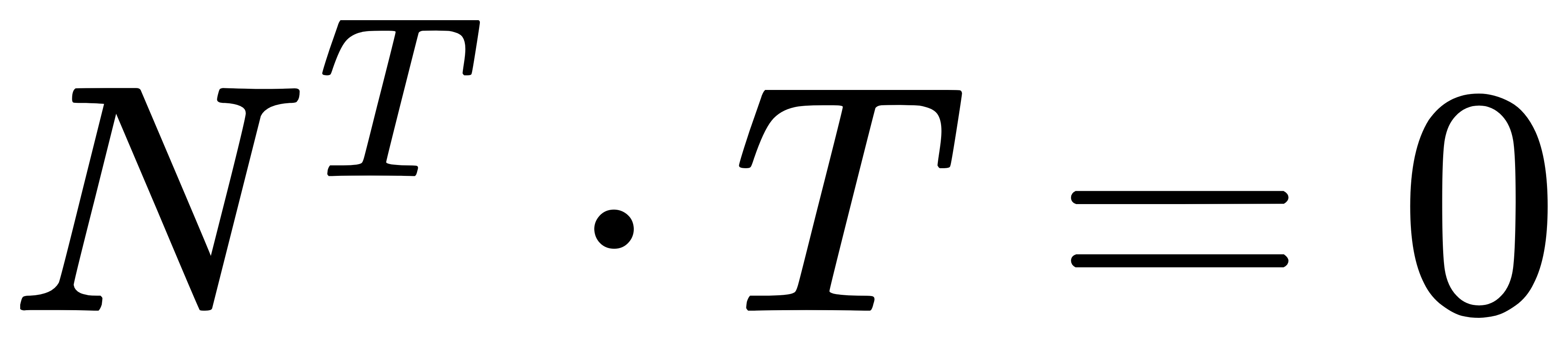
这里使用了一个非常讨巧的办法,引入了一个单位矩阵。假设我们对顶点进行的变换其矩阵为M,那么我们有以下的恒等变换:
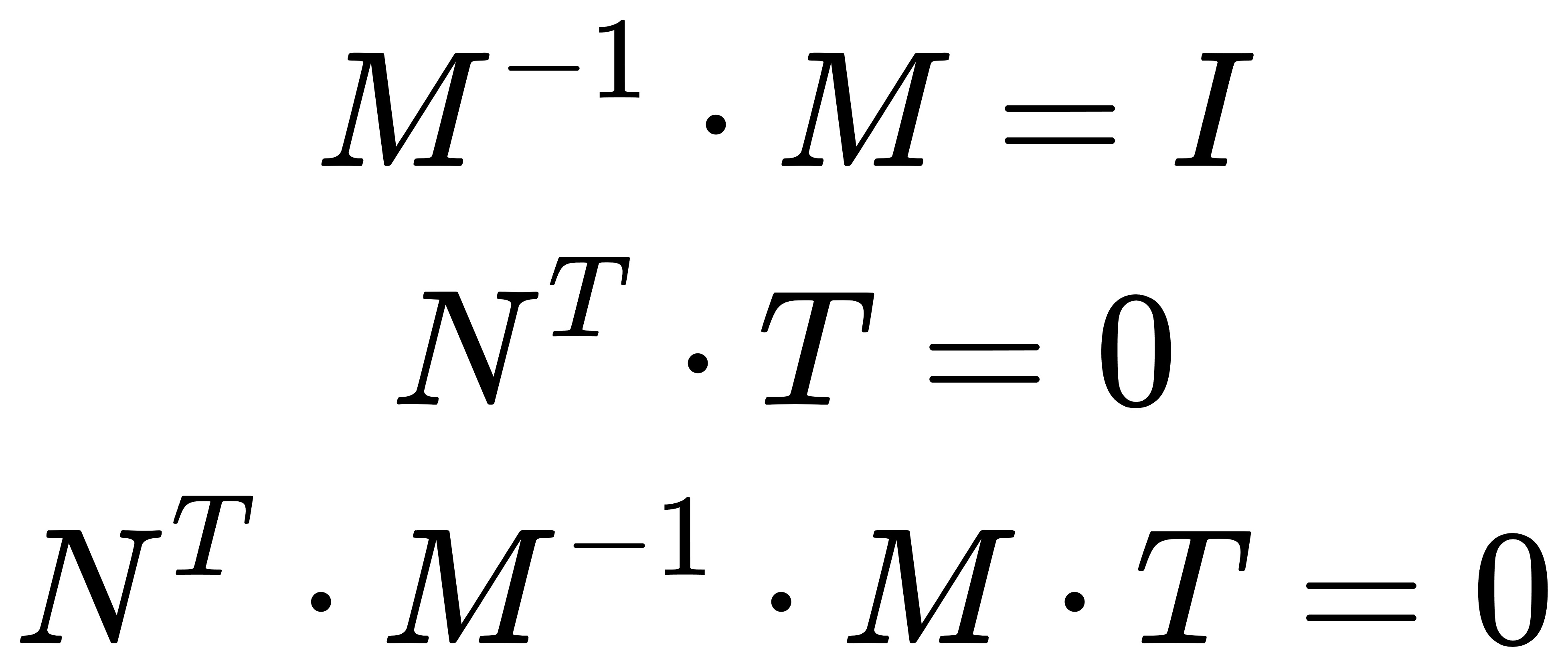
其中,我们可以将这个恒等变换分为两部分:
(1)顶点变换
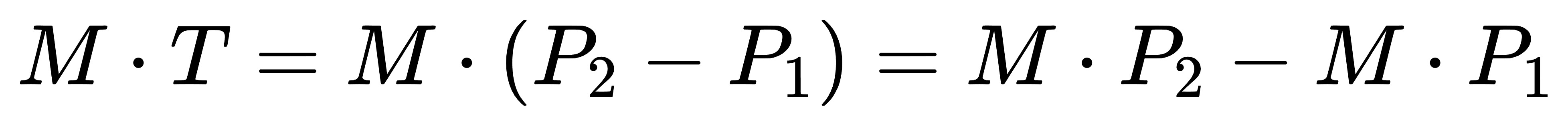
不难发现,右侧的部分相当于对点P1和P2进行了M变换以后,新顶点构成的三角面中的一个向量。
(2)法向变换
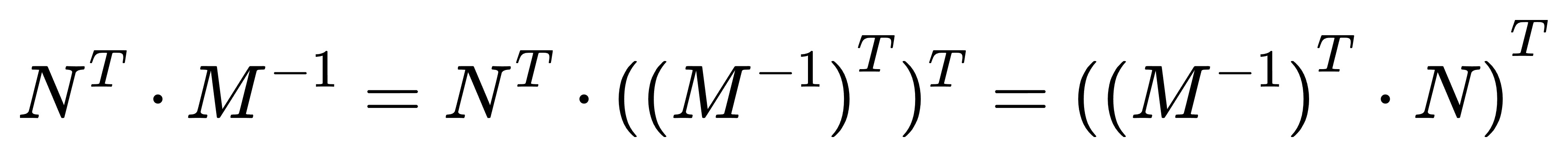
对左侧部分进行变形就可以发现,其实左侧部分刚好就是对法向的变换。另外,这样的恒等变换保持了变换前后法向依然垂直于三角面(变换后的法向与三角面中任意两点组成的向量点积为0)。
由此,我们可以得到以下结论:如果对顶点进行变换M,则对法向的变换矩阵为M逆矩阵的转置。
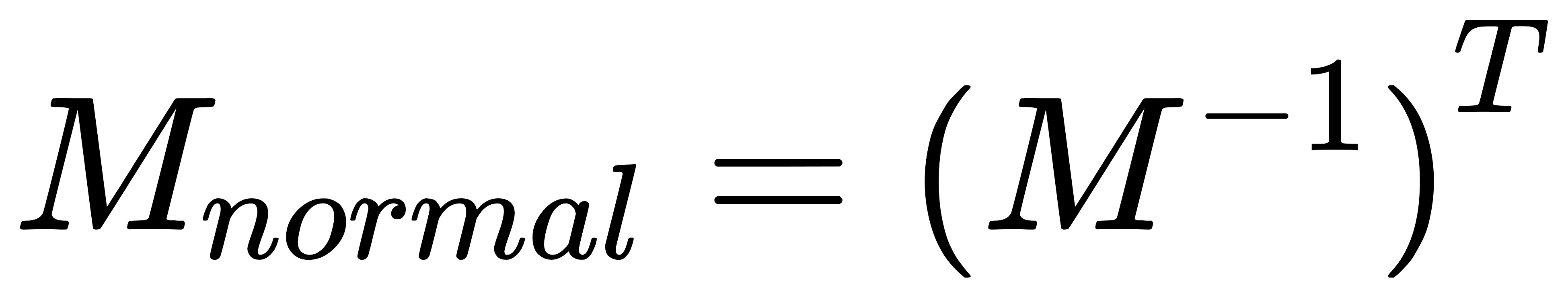









Comments | 1 条评论
不来点vulkan教程吗?