二分查找边界问题分析

概述

　　二分查找对于有序序列性能非常优越，能够达到O(logn)级别，因此熟练使用二分搜索是非常重要的。但是，正如Knuth评价的那样：
　　Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…
　　意思是说，尽管二分搜索算法的基本思想比较简单，但是细节却非常棘手。我觉得这样的评价真的是非常客观而且到位的，如果不花点心思研究一下二分搜索算法的边界问题，还真的很难做到熟练使用二分搜索算法。这里，我就把自己学习时候的理解和体会作以总结和分析。

二分查找的基本思路

　　最基本的二分查找算法的实现如下代码所示：对一个有序序列而言（我们此处只讨论非递减序列）对于某个要查找的值，我们每次取搜索区间的中间位置，根据中间位置来决定下一步该如何做，则可以分为以下三种情况：
　　1.如果中间位置的值是我们要查找的值，则返回对应的下标
　　2.如果中间位置的值比我们要查找的值小，则可以推出我们要查找的值在搜索区间的后半部分，更新搜索区间即可（因为序列非递减）
　　3.如果中间位置的值比我们要查找的值大，则可以推出我们要查找的值在搜索区间的前半部分，更新搜索区间即可
　　4.重复上述步骤，直到找到查找值，或者区间长度小于0（即搜索区间不存在）则未找到。

//a[]为要搜索的数组，n表示数组的长度，x表示要搜索的值
int BinarySearch(int a[],int n,int x){
    int left=0,right=n-1;               //初始化区间长度
    while(left<=right){                 //当区间长度大于0时，进行循环，假如循环一直走到尽头，则循环结束时，显然有left=right+1
        int mid=left+(right-left)/2;    //取中间位置，这里的写法可以避免left+right溢出的情况发生
        if(a[mid]==x)                   //如果找到查找值，返回下标
            return mid;
        else if(a[mid]>x)               //如果中间位置的值大于目标值，则向前半部分查找，此时收缩右边界，因为mid位置已经判定过，故right=mid-1
            right=mid-1;
        else if(a[mid]<x)               //如果中间位置的值小于目标值，则向后半部分查找，此使收缩左边界，因为mid位置已经判定过，故left=mid+1
            left=mid+1;
    }                                   //如果查找失败，则必有left之前的所有值都<x，即left所在的位置为x需要插入的位置
    return left;      
}

　　注意：我这里特别强调了left最后所在位置的特征，这对于理解边界情况非常有帮助，请仔细理解left下标之前的所有值都小于x。

二分查找的边界情况

　　如果非递减序列中，查找的目标值有多个，则有时候我们需要找到这个重复值的左边界和重复值的右边界（如果此值存在的情况下），如下图所示：

二分查找的左边界

　　在理解算法的写法之前，我们先来简单分析和理解一下左边界的特征和规律，不难发现左边界的下标之前的所有值都是小于目标值的，也就是说我们只要按照二分的思路找到那个左侧所有值都小于目标值，右半部分都大于等于目标值的位置即可。这与二分查找的基本思路还是有很大相似之处的，有一点不同在于如果中间值等于目标值的时候，我们不需要返回而是需要更新区间范围的右侧，直到循环结束。
　　这里先给出代码实现，然后来逐一讲解其中的细节：

//左边界的二分查找
int LeftBinarySearch(int a[],int n,int x){
    if(n<=0) return -1;                 //如果数组为空直接返回查找失败
    int left=0,right=n-1;               //区间初始化
    while(left<=right){                 //当区间长度不为0的时候循环
        int mid=left+(right-left)/2;    //取中间位置
        if(a[mid]==x)                   //如果相等，向左缩小范围，更新right
            right=mid-1;
        else if(a[mid]>x)               //如果大于，也向左缩小范围，更新right
            right=mid-1;
        else if(a[mid]<x)               //如果小于，正常向右做小范围，更新left
            left=mid+1;
    }                                   //最终left的左侧都是小于x的值，循环结束后right=left-1
    return (left>=n||a[left]!=x)?-1:left;//假如有0个，则left为0（不越界），假如有n个则left=n，则需要判断边界。判断边界和存在性，并返回结果
}

　　循环结束后，必有right=left-1（即区间长度小于1），此时的left所在位置左侧值都小于目标值，left（包含left）之后的值都是大于等于目标值的，但是个别情况下又有些细微的区别，我们一一来看：
　　这里我们给出一个非递减序列，查找目标值为16
　　情况一：
　　正常情况下，小于16的值有5个，最终left会停留在5。此时，如果值存在，就是左边界；如果不存在则查找失败（因此最终找到left后要对存在性做验证）。
　　情况二：
　　如果小于16的值有0个（即0号位置便是大于等于16的值），则最终left会停留在0处。显然0是一个合法值，所以只需要在最后对存在性做验证即可。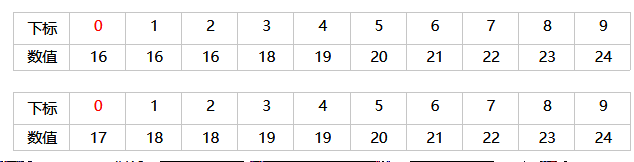
　　情况三：
　　如果小于16的值有n个（即所有的值都小于16），则最终left会停留在n处。显然left=n对于数组访问来说是一个非法值，所以需要特判，此种情况为查找失败。
　　综上三种情况：
　　我们只需要当中间值小于x的时候更新left，其他时候更新right，那么left最终停留的位置左侧值都小于目标值，left（包含left）之后的值都大于等于目标值，因此获得left之后，只需要判定是不是等于n（不合法下标）和存在性检验即可，如果越界或者不存在都认为查找失败，否则正常返回左边界。
　　故代码实现上，我们可以稍作合并，如下所示：

//左边界的二分查找，稍作简化
int LeftBinarySearch(int a[],int n,int x){
    if(n<=0) return -1;                 //如果数组为空直接返回查找失败
    int left=0,right=n-1;               //区间初始化
    while(left<=right){                 //当区间长度不为0的时候循环
        int mid=left+(right-left)/2;    //取中间位置
        if(a[mid]>=x)                   //如果中间值大于等于x，则更新right
            right=mid-1;
        else if(a[mid]<x)               //如果中间值小于x，则更新left
            left=mid+1;
    }                                   //最终left的左侧都是小于x的值，循环结束后right=left-1
    return (left>=n||a[left]!=x)?-1:left;//对最终的left合法性和存在性检验
}

二分查找的右边界

　　同样的在实现代码之前，我们先来简单分析和理解一下右边界的特征和规律，容易发现右边界的下标之前的所有值都是小于等于目标值的，同理，只要我们找到到那个左侧所有值都小于等于目标值，右半部分都大于目标值的位置即可。同样的情况，如果中间值等于目标值的时候，我们不需要返回而是需要更新区间左侧，直到循环结束。
　　这里，为了方便记忆，且左右有别，我们在右边界的情况下，返回值关注right，虽然依旧是以left为关注点来研究，但是最终right=left-1很好换算，所以右边界关注，更加贴合右边界的记忆逻辑。
　　这里也先给出代码实现，然后来逐一讲解其中的细节：

//右边界的二分搜索
int RightBinarySearch(int a[],int n,int x){
    if(n<=0) return -1;                 //如果数组为空直接返回查找失败
    int left=0,right=n-1;               //区间初始化
    while(left<=right){                 //当区间长度不为0的时候循环
        int mid=left+(right-left)/2;    //取中间位置
        if(a[mid]==x)                   //当等于的时候，向右缩小范围，更新left
            left=mid+1;
        else if(a[mid]>x)               //当大于时，向左压缩范围，更新right
            right=mid-1;
        else if(a[mid]<x)               //当小于的时候向右压缩范围，更新left
            left=mid+1;
    }                                   //最终left的左侧都是小于等于x的值，循环结束时，right=left-1
    return (right<0||a[right]!=x)?-1:right;//假如有0个小于等于x的值，left=0，则right为-1，不能取数组下标，所以需要特判，如果有n个则left最后等于n，而right等于n-1不会越界，只需验证存在性
}

　　循环结束后，必有right=left-1（即区间长度小于1），此时的left所在位置左侧值都小于等于目标值，left（包含left）之后的值都是大于目标值的，仍然是个别情况下又有细微的区别：
　　还是我们给出一个非递减序列，查找目标值为16
　　情况一：
　　正常情况下，小于等于16的值有8个，最终left会停留在8。此时，如果值存在，就是right=left-1便是右边界；如果不存在则查找失败（因此最终找到left后要对存在性做验证）。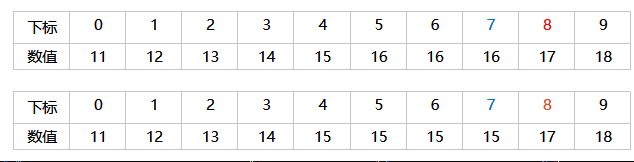
　　情况二：
　　如果小于等于16的值有0个（即0号位置便是大于16的值），则最终left会停留在0处，而right=left-1=-1，显然-1对于数组访问来说是一个非法值，所以需要特判。
　　情况三：
　　如果小于16的值有n个（即所有的值都小于等于16），则最终left会停留在n处。而right=left-1=n-1，显然right的值是合法的，所以只需要做存在性判断即可。
　　综上三种情况：
　　我们只需要当中间值小于等于x的时候更新left，其他时候更新right，那么left最终停留的位置左侧值都小于等于目标值，left（包含left）之后的值都大于目标值，此时right=left-1，因此获得right之后，只需要判定会不会等于-1（不合法下标）和存在性检验即可，如果越界或者不存在都认为查找失败，否则正常返回右边界。
　　故代码实现上，我们可以稍作合并，如下所示：

//右边界的二分搜索，稍作简化
int RightBinarySearch(int a[],int n,int x){
    if(n<=0) return -1;                 //如果数组为空直接返回查找失败
    int left=0,right=n-1;               //区间初始化
    while(left<=right){                 //当区间长度不为0的时候循环
        int mid=left+(right-left)/2;    //取中间位置
        if(a[mid]<=x)                   //当中间值小于等于x的时候，更新left
            left=mid+1;
        else if(a[mid]>x)               //其他情况，更新right
            right=mid-1;
    }                                   //最终left的左侧都是小于等于x的值，循环结束时，right=left-1
    return (right<0||a[right]!=x)?-1:right;//对获得的right进行合法检测和存在性检测
}