树与二叉树
为了直观的体验不同的数据结构的样子和相关操作,推荐参考数据结构和算法的可视化网站Visualgo选择相应的类型通过动画和伪代码的形式观察和学习。
树和二叉树的实现以及基本的遍历方法和代码,包括一般树(多叉树)的静态表示方法和遍历,以及二叉树的存储实现和遍历代码。
用到的头文件有如下两个:
#include<queue>
#include<vector>树的实现和遍历
树的实现
这里的树指的是,一般意义的树,多叉且孩子没有顺序的区别.
这里采用树的静态写法作示例:
//静态写法
#define MAXN 1000 //最大的结点个数
struct node{
int data;
//int child[MAXN]; //指针域,存放所有孩子的指针,可以用vector来代替定长数组,如下所示
vertor<int> child;
}Node[MAXN] //MAXN表示树中的结点上限基于静态写法的新结点的创建
//静态写法中创建新结点
int index=0; //初始化树为空,可用结点下标为0
int newnode(int v){
if(index >= MAXN) return -1; //判定是否有可用的空结点,如果没有返回-1,代表结点申请失败
Node[index].data = v;
Node[index].child.clear();
return index++; //返回创建的结点的下标,然后index自增,为下一次申请新结点的判定作准备
}树的遍历
树的先根遍历,因为多叉树的孩子数量不定,因此没有中序和后序遍历的说法。
//树的先根遍历
void preorder(int root){
printf("%d",Node[root].data); //访问当前结点
for(int i = 0;i < Node[root].child.size(); i++){ //依此先根遍历所有的孩子结点
preorder(Node[root].child[i]);
}
}树的层次遍历
//树的层次遍历
void layerorde (int root){
queue<int> q; //借助队列实现层次遍历
q.push(root); //根节点入队
while(!q.empty()){ //队不空时进行循环
int now =q.front(); //去除队头元素并访问
q.pop;
printf("%d",Node[now].data);
for(int i = 0;i < Node[now].child.size(); i++){ //将当前结点的所有孩子按照先后顺序入队
q.push(Node[now].child[i]);
}
}
}二叉树
二叉树的存储
静态储存结构,使用数组存储结点结构体,使用数组下标表示指针,其中可以用-1(任何负数都可以)表示空指针,其基本的操作和链式差不多。
链式存储结构,使用结构体表示一个二叉树的结点,包括数据域、指针域、以及可能用得到的记录结点所在的层次的变量。
typedef struct node{
int data;
int layer; //如果需要在层次遍历中用到结点,可以添加一个记录层次的成员变量
struct node *lchild,*rchild; //左右孩子的指针域
}Node,*Tree;相关的基本操作
1.创建新结点
创建新结点
Node* newnode(int v){ //创建一个结点值为v的结点
Node * new_node = new node; //创建一个新的结点,用new_node指针变量指向
new_node->data=v; //赋值
new_node->lchild=new_node->rchild=NULL; //左右孩子指针域初始为空
return new_node;
}2.二叉树结点的查找和修改
二叉树结点的查找和修改
//查找结点值为x的结点,并修改为newdata
void search(Node * root, int x, int newdata ){
if(root == NULL){
return; //递归边界,如果是空的则返回
}
if(root->data == x){
root->data=newdata; //如果找到x所在的结点,更新为新的值
}
//递归调用,分别往左右子树搜索x并修改
search(root->lchild, x, newdata);
search(root->rchild, x, newdata);
}3.二叉树结点的插入
二叉树结点的插入
二叉树的插入和二叉树本身的特征有关,此处只给出伪代码:
//使用insert向二叉树中插入一个值为x的结点
//树的指针要使用引用,否则插入的修改操作不起作用
void insert(Node* &root, int x){
if(root == NULL){ //如果树空,直接创建一个结点插入
root=newnode(x); //调用新建结点函数
return;
}
if( 由二叉树自身的性质决定判定,x插入在左子树){
insert(root->lchid, x);
}
else{
insert(root->rchild, x);
}
}4.二叉树的建立
二叉树的建立
二叉树的创建,借助插入函数,每次读入一个结点,然后插入即可。
//使用一个数组序列data[]建立二叉树
Node* Creat(int data[],int n){
Node* root=NULL; //创建根结点
for(int i = 0; i < n; i++){ //将数据序列依此插入到二叉树中
insert(root,data[i]);
}
return root;
}5.二叉树的比较
二叉树的比较
二叉树的比较,即判断两棵二叉树是否完全相同。二叉树的比较又可以细分为两种:判断相同的二叉树比较、判断同构的二叉树比较。
判断相同的二叉树比较即判断二叉树是否完全相同,包括二叉树的左右子树关系和次序,结点的元素个数等等,均要求相同才相同。使用递归的判断方法:
bool Campare(Node* root1, Node* root2)
{
bool ret=false; //单一的返回出口,默认为false,默认两棵树不相同
if(root1==NULL&&root2==NULL) //如果两棵树都是空树,判断两棵树相同
ret=true;
else if(root1!=NULL&&root2!=NULL&&root1->data==root2->data) //如果两棵树都不会空,且结点值相同,递归判定左右子树是否都相同
ret=Campare(root1->lchild,root2-l>child)&&Campare(root1->rchild,root2->rchild); //当左右子树都相同时才判断两棵树相同
return ret;
}判断同构的二叉树比较,即任意交换一棵二叉树中某一对或几对二叉树的左右子树得到的新的树,认为和原来的二叉树是同构的。同构的二叉树有一个特征,父子关系不变,只是改变了某几对二叉树左右子树的顺序,因此,采用并查集的方法能够思路清晰的判定是否同构。代码如下:
#include<bits/stdc++.h>
using namespace std;
//使用并查集判断树的同构,以上头文件是PAT刷题模板,为了尽可能包含所有可能用到的头文件
//本例采用数组的方式用并查集记录父子关系,然后转化为用map存储,由于map会自动排序,方便比较。
typedef struct{
char data; //结点的值
int fa; //该结点父节点在数组中的下标
}Node;
map<char,char> mp1; //使用map记录两棵树每个结点指向父节点的映射
map<char,char> mp2;
void CreatTree(map<char,char> &mp); //根据树,建立map记录
int main(){
CreatTree(mp1);
CreatTree(mp2);
if(mp1==mp2) //如果两个map记录的父子对应关系完全相同,说明两棵树同构,否则不同构
puts("Yes");
else
puts("No");
return 0;
}
void CreatTree(map<char,char> &mp)
{
int n;
char a,b,c;
cin>>n;
vector<Node> v(n); //使用并查集记录二叉树结点的父节点的编号
getchar(); //吸收多余的回车字符
for(int i=0;i<n;i++){ //初始化父结点为-1
v[i].fa=-1;
}
for(int i=0;i<n;i++){
scanf("%c %c %c",&a,&b,&c);
getchar();
v[i].data=a;
if(b!='-') v[b-'0'].fa=i; //当有左右孩子时,给其孩子添加父节点标记
if(c!='-') v[c-'0'].fa=i;
}
for(int i=0;i<n;i++){ //用map容器记录父子关系
int index=v[i].fa;
if(index==-1) //如果没有父节点就是根节点,映射为特殊字符#
mp[v[i].data]='#';
else
mp[v[i].data]=v[index].data;//如果有父节点,就映射为其父节点的值
}
}
/*
题目测试数据输入格式
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的
测试数据输入样例1
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
样例1输出结果
Yes
测试数据输入样例2
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
样例2输出结果
No二叉树的遍历
二叉树的先序、中序、后序遍历路径其实是相同的。如下图所示,先序为路径上第一次遇到时就访问,中序是路径上第二次遇到访问,后序为第三次遇到时访问。
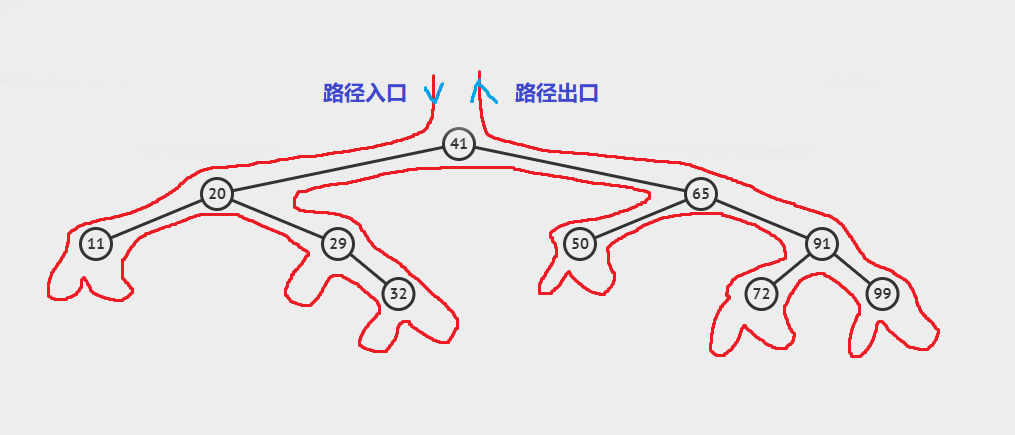
其中,由于叶子结点有两个空指针域,故算上相应的遍历和返回次数,可以按照遇到先后的次序不同得到不同的遍历序列。
先序遍历
先序遍历的递归写法:
//先序遍历的递归写法
void preorder(Node * root){
if(root == NULL) return; //递归边界
printf("%d/n",root->data); //先序访问结点
preorder(root->lchild); //递归先序遍历左子树
preorder(root->rchild); //递归先序遍历右子树
}先序遍历的非递归写法:借助栈实现先序的遍历,在第一次遇到时进行访问。代码如下:
//先序遍历的非递归写法
//使用了stack容器,需要包含头文件
#include<stack>
void preorder(Node* root){
stack<Node*> s;
Node *p=root; //p为遍历指针
while(p||!s.empty()){ //当栈不空时或者p不为空时进行循环
if(p){
visit(p); //第一次遇到,访问结点,具体的访问函数视需求而定
s.push(p); //将根进栈,遍历左子树
p=p->lchild;
}
else{
p=s.top();
s.pop(); //如果p是空,说明到达了最左边的结点,此时p出栈,转向右子树继续遍历。
p=p->rchild;
}
}
}中序遍历
中序遍历的递归写法:
//中序遍历的递归写法
//与先序相似,只不过改动了访问的顺序
void inorder(Node * root){
if(root == NULL) return; //递归边界
inorder(root->lchild); //递归中序遍历左子树
printf("%d/n",root->data); //中序访问结点
inorder(root->rchild); //递归中序遍历右子树
}中序遍历的非递归写法:借用栈实现,与先序非常相似,知识调整了visit()的位置,放在第二次遇到时进行访问,代码如下:
//中序遍历的非递归写法
//使用了stack容器,需要包含头文件
#include<stack>
void inorder(Node* root){
stack<Node*> s;
Node *p=root; //p为遍历指针
while(p||!s.empty()){ //当栈不空时或者p不为空时进行循环
if(p){
s.push(p); //将根进栈,遍历左子树
p=p->lchild;
}
else{
p=s.top();
s.pop(); //如果p是空,说明到达了最左边的结点,此时p出栈,转向右子树继续遍历。
visit(p); //第二次遇到,访问结点,具体的访问函数视需求而定
p=p->rchild;
}
}
}后序遍历
后序遍历的递归写法:
//后序遍历的递归写法
//与先序相似,只不过改动了访问的顺序
void postorder(Node * root){
if(root == NULL) return; //递归边界
postorder(root->lchild); //递归后序遍历左子树
postorder(root->rchild); //递归后序遍历右子树
printf("%d/n",root->data); //后序访问结点
} 后序遍历的非递归算法,主要的难点在于如何区分是第二次遇到还是第三次遇到(即,是从左子树返回还是右子树返回),因此采用不同地解决方法,得到两种遍历算法的思路:
第一种:需要一个指针来分清是第二次遇到(从左子树返回)还是第三次遇到(从右子树返回),用辅助指针r指向最近访问过的最近的结点(即,遍历路径上某个访问点的前驱结点)。
第二种:采用带标记栈的方法,来记录当前结点的左右子树是否被访问过,用以区分是从左子树返回,还是右子树返回。
一、采用栈+额外指针的方式实现非递归算法,代码如下:
//后序遍历的非递归写法,采用栈和额外指针的方法
#include<stack>
void postorder(Node* root){
stack<Node*> s; //栈
Node* p=root; //p为工作指针
Node* r=NULL; //用于记录上一个结点的辅助指针,初始化为空
while(p||!s.empty()){
if(p){
s.push(p); //一直向左到最左边的结点
p=p->lchild;
}
else{
p=s.top(); //到边界空指针时,转回父节点
if(p->rchild&&p->rchild!=r){ //当右指针不空,且前一个结点不是右孩子(即,不是从右孩子返回,而是从左孩子返回)
p=p->rchild; //转向右子树,一直到右子树的做左边
s.push(p);
p=p->lchild;
}
else{ //否则右子树为空(也认为是直从右子树返回)或者右子树不为空且从右子树返回
p=s.top(); //从右子树返回(即第三次遇到)进行访问
s.pop();
vist(p); //访问的操作函数要求写
r=p; //记录最近访问的结点
p=NULL; //p置空,表示当前结点的子树全部访问完毕,以起到类似返回的效果,驱动从栈中取元素出来
}
}
}
}二、采用标记栈方法的后序遍历的非递归算法
//采用标记栈方法的后序遍历的非递归算法
#include<stack> //需要包含stack头文件
typedef struct{ //定义标记栈中元素的存储结构体
Node* p; //二叉树结点指针
int rvis; //访问标记,0表示表示右子树未被访问,1表示右子树已被访问
}Snode;
void postorder(Node* root){
Snode sn; //用去取栈中元素
stack<Snode> s; //建立栈
Node* pt=root; //二叉树的遍历工作指针
//为了让下边出栈遍历的循环层次看起来少一些,将一直走到左边的循环单独写出来
while(pt){ //一直走到最左边
Snode temp; //用于构建临时的栈元素,用于入栈
temp.p=pt;
temp.rvis=0;
s.push(temp);
pt=pt->lchild;
}
while(!s.empty()){
sn=s.top(); //读取栈顶元素
if(sn.p->rchidl==NULL || sn.rvis==1){
vist(sn.p); //如果右子树为空(认为直接返回)或者右子树已被访问(即,从右子树返回,第三次遇到),进行出栈访问;
s.pop();
}
else{ //否则转向右子树
sn.rvis=1; //修改右子树访问标记
pt=sn.p->rchidl;
while(pt){ //在右子树中走到最左下方
Snode temp; //用于构建临时的栈元素,用于入栈
temp.p=pt;
temp.rvis=0;
s.push(temp);
pt=pt->lchild;
}
}
}
}层次遍历
层次遍历,借助队列实现:先把根结点入队,然后每次从队列中取出一个结点,如果左右子树不为空,就把左右子树入队,一直循环到队列为空。代码如下:
//使用队列的层次遍历
#include<queue> //需要包含queue头文件
void layerorder(Node* root){
queue<node*> q; //队列中存放树的结点指针
q.push(root); //根结点入队
while(!q.empty()){
Node* now; //依此从队列中取出队头元素,进行访问
now=q.front();
q.pop();
printf("%d\n",now->data);
//如果左右孩子不空,左右孩子入队
if(now-lchild) q.push(now->lchild);
if(now-rchild) q.push(now->rchild);
}
}二叉树遍历的应用
由遍历序列建树
给定二叉树的中序遍历序列和(先序、后序、层次遍历)的任意一个遍历序列可以构建唯一的二叉树,其中中序遍历序列必不可少,因为参照中序序列可以分开左右子树。
此处以先序+中序为例,后序序列的方法类似,找到根节点以后在中序中定位根节点,并对左右子树递归调用建立树,难点在于对递归时在序列中的位置的计算,代码实现如下:
//一直先序和中序的遍历序列,建立二叉树
int pre[MAXN]; //先序遍历序列
int in[MAXV]; //中序遍历序列
Node* creat(int pl, int pr, int il, int ir){
//pl和pr分别代表先序的左边和右边下标
//il和ir分别代表后序的左边和右边下标
if(pl>pr) return NULL; //递归边界,先序长度小于或者等于0时返回空指针
Node* root=new node; //创建一个新结点用于存放二叉树的根
root->data=pre[pl];
int k;
for(k=il; k<=ir ; k++){ //在中序序列中寻找根节点的位置k,k左侧是左子树,k右侧是右子树
if(in[k] == pre[pl]) break;
} //可以采用unordered_map建立中序序列和下标的映射,方便快速查询k的位置
int numleft=k-il; //左子树的结点数量
//根据左子树结点的个数,确定左右子树对应的先序和后序的下标位置,然后递归建立左右子树
root->lchild=creat(pl+1,pl+numleft,il,k-1);
root->rchild=creat(pl+numleft+1,pr,k+1,ir);
return root; //返回创建树的根节点
}二叉搜索树(BST)
二叉树的基本定义和特征:
(1)为空树;
(2)或者左、右子树为二叉搜索树;
(3)左子树的元素都小于根,右子树的元素都大于根(或者,左子树的元素都大于根,右子树的元素都小于根);
由上可知,二叉树的重要特征:中序遍历得到的序列是有序的。
二叉搜索树的插入和建立
二叉搜索树的插入和建立过程与一般的二叉树基本相同,插入时的判定为:
//如果有重复的元素插入,则需判断是否等于根结点的值,如果等于,不用插入,直接返回
if(x<root->data)
insert(root->lchild,x); //如果小于根结点,插入到左子树
esle
insert(root->rchild,x); //如果大于根结点,插入到右子树删除结点
删除二叉搜索树的几点采用的方法是:如果是叶子结点,则直接删除;如果不是叶子结点,寻找该结点的左子树中最大(即中序遍历的前驱)的或者右子树中最小(即中序遍历中的后继)的结点替代该结点,然后递归删除用来替换的结点。
首先需要两个函数分别寻找最大值和寻找右最小值:
//寻找最大
Node *findmax(Node * root){
while(root->rchild!=NULL){ //根据二叉搜索树的性质,一直向右子树走便是最大
root=root->rchild;
}
return root;
}
//寻找最小
Node *findmin(Node * root){
while(root->rchild!=NULL){ //根据二叉搜索树的性质,一直向左子树走便是最小
root=root->rchild;
}
return root;
}
//删除二叉搜索树的结点
void deleteNode(Node * &root,int x)
{
if(root==NULL) return; //如果不存在值为x的结点,直接返回
if(root->data==x){ //如果找到值为x的结点
if(root->rchidl==NULL&&root->rchild==NULL) //如果是叶子结点,直接删除
root=NULL;
else if(root->lchid!=NULL){ //如果不是叶子结点,且存在左子树
Node *pre=findmax(root->lchild); //找到前驱节点,即左子树中的最大结点
root->data=pre->data; //用前驱结点替换
deleteNode(root-lchild,pre->data); //递归在左子树中删除前驱结点
}
else{
Node *next=findmin(root->rchild); //找到后继节点,即右子树中的最小结点
root->data=next->data; //用后继结点替换
deleteNode(root-rchild,next->data); //递归在右子树中删除后继结点
}
}
else if(x>root->data)
deleteNode(root->rchild,x); //如果x大于当前结点,则递归在右子树中删除
else
deleteNode(root->lchild,x); //如果x小于当前结点,则递归在左子树中删除
}小结,在上述的删除算法中有一个缺陷,由于优先考虑使用前驱结点替换,所以有可能导致树中的结点偏向一边。对此,有两种解决办法:一、当被删除的结点的左右子树都存在的时候,使用随机数决定用前驱还是后继来替换。二、采用结构更加优秀的平衡二叉树(AVL)。
平衡二叉树(AVL)
平衡二叉树的定义
平衡二叉树本身仍然是一棵二叉搜索树,但是为了解决二叉搜索树插入过程中可能导致不平衡的问题,引入一个指标平衡因子,(即,某个节点的左子树与右子树的高度差)。于是,有了平衡的概念,所有结点的平衡因子绝对值都不超过1,则认为该二叉搜索树平衡,即为平衡二叉树(AVL)。
平衡二叉树的结点定义
平衡二叉树的由于有了平衡因子的概念,因此对于结点的定义,需要增加与之相关的结构体成员。在结点中增加一个表示以当前结点为根结点的树的高度high
//结点定义
typedef struct node{
int data,high; //结点的数据和高度
struct node *lchild,*rchild;
}Node,*Tree;
//新建结点的函数
Node *newnode(int x){
Node * root=new Node;
root->data=x; //结点赋值
root->high=1; //高度初始化为1,空结点的高度定义为0,因此单个结点的高度为1
root->lchild=root->rchild=NULL;
return root;
}平衡二叉树的平衡因子
平衡因子,通过结点的左右子树的高度计算得出:
//通过以下函数得到某个结点的高度
int gethigh(Node *root){
if(root==NULL) return 0; //空结点高度为0
else return root->high;
}
//通过一下函数获得得到某个结点的平衡因子(BalanceFactor),简写为bf
int getbf(Node *root){
return gethigh(root->lchild)-gethigh(root->rchild); //平衡因子等于左子树减去右子树的高度
}
//当插入时,更新某个结点的高度
void updatehigh(Node *root){
root->high=max(gethigh(root->lichild),gethigh(root->rchild))+1; //根结点的高度等于左右子树中的较大值加 1
}平衡二叉树的插入
平衡二叉树的插入和一般二叉搜索树的插入比较类似,只是在二叉搜索树的插入基础上增加了调整平衡的步骤。
平衡二叉树的调整
* 本小节图片引用自《算法笔记》,可以阅读原书讲解,加深理解
左旋与右旋
平衡二叉树的调整有两种形式:左旋和右旋。
左旋及其代码如下所示:
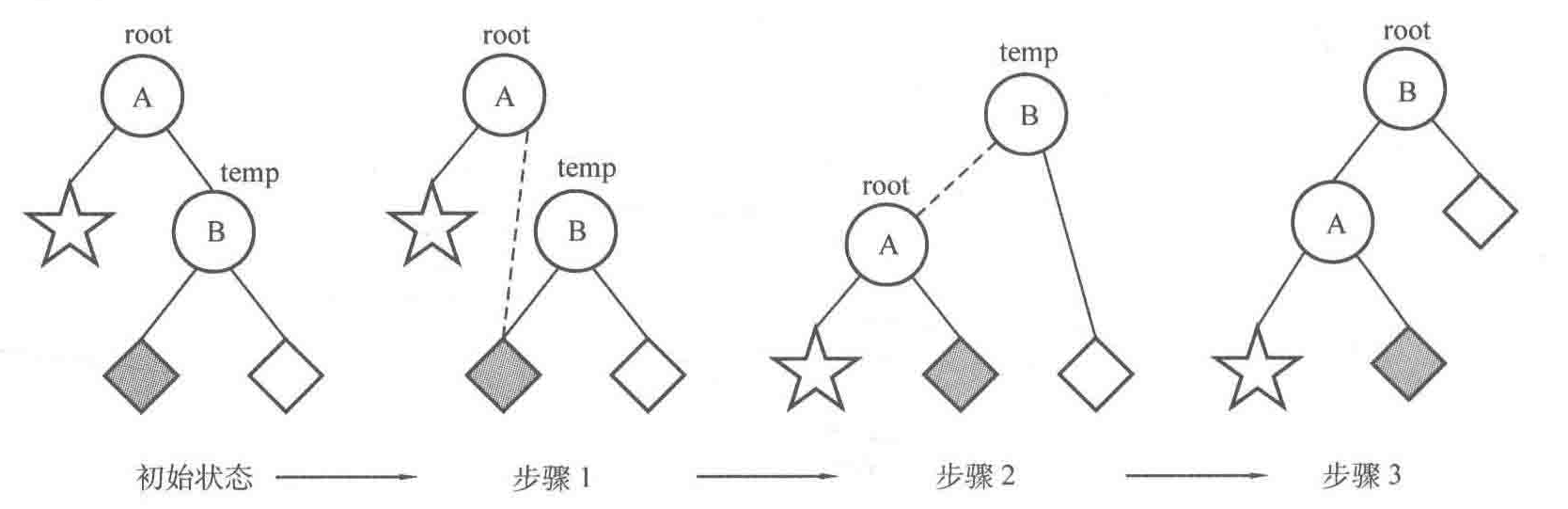
//左旋
void L(Node *&root){ //因为需要修改指针,因此要传引用
Node *temp=root->rchild;
root->rchild=temp->lchild; //步骤1
temp->lchild=root; //步骤2
updatehigh(root); //更新结点的高度
updatehigh(temp);
root=temp; //步骤3
} 右旋及其代码如下所示:

//右旋
void R(Node * &root)
{
Node *temp=root->lchild;
root->lchild=temp->rchild;
temp->rchild=root; //步骤1
updatehigh(root); //步骤2
updatehigh(temp);
root=temp; //步骤3
}左旋与右旋的使用
左旋和右旋的使用,用于在插入时调整树的平衡。主要有一下类型:LL型、LR型;RR型,RL型。
LL型的调整,只需要对平衡因子为2的树使用右旋(R):

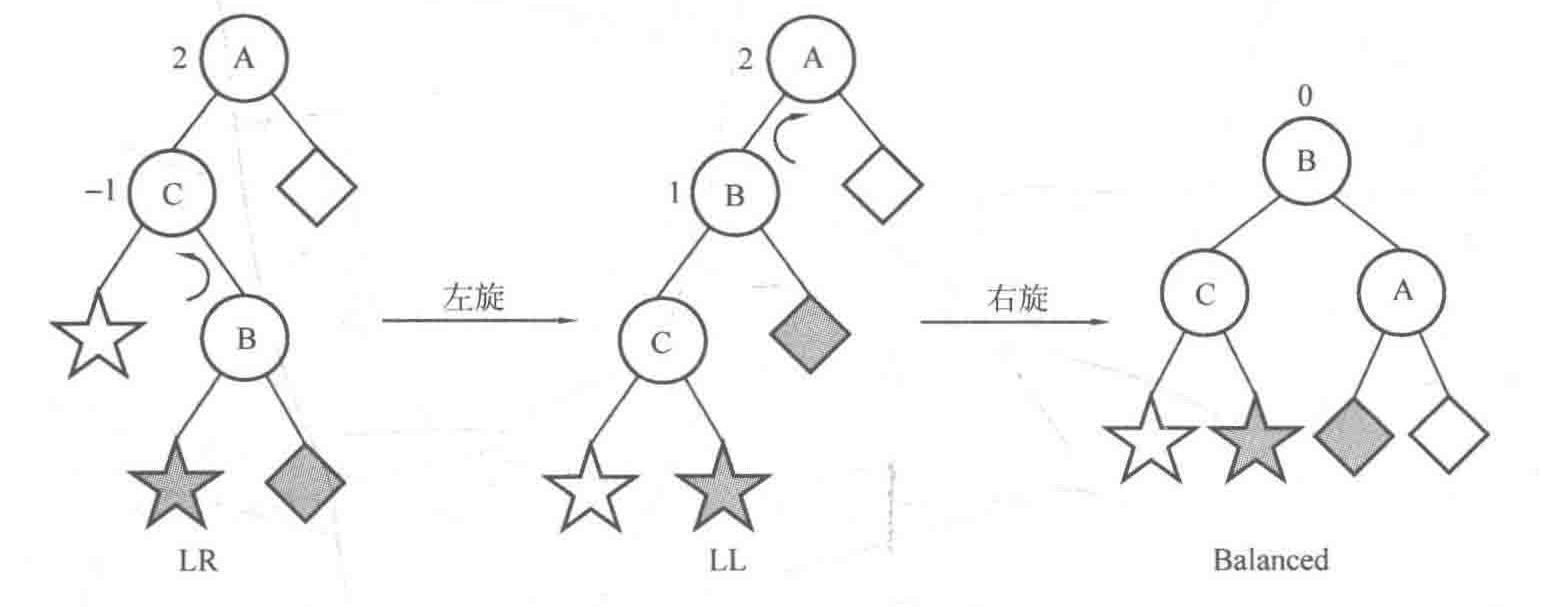
LR型的调整,先要对子树中平衡因子为-1的左子树使用 左旋(L) 变成LL型,再对平衡因子为2的结点使右旋(R) 即可:
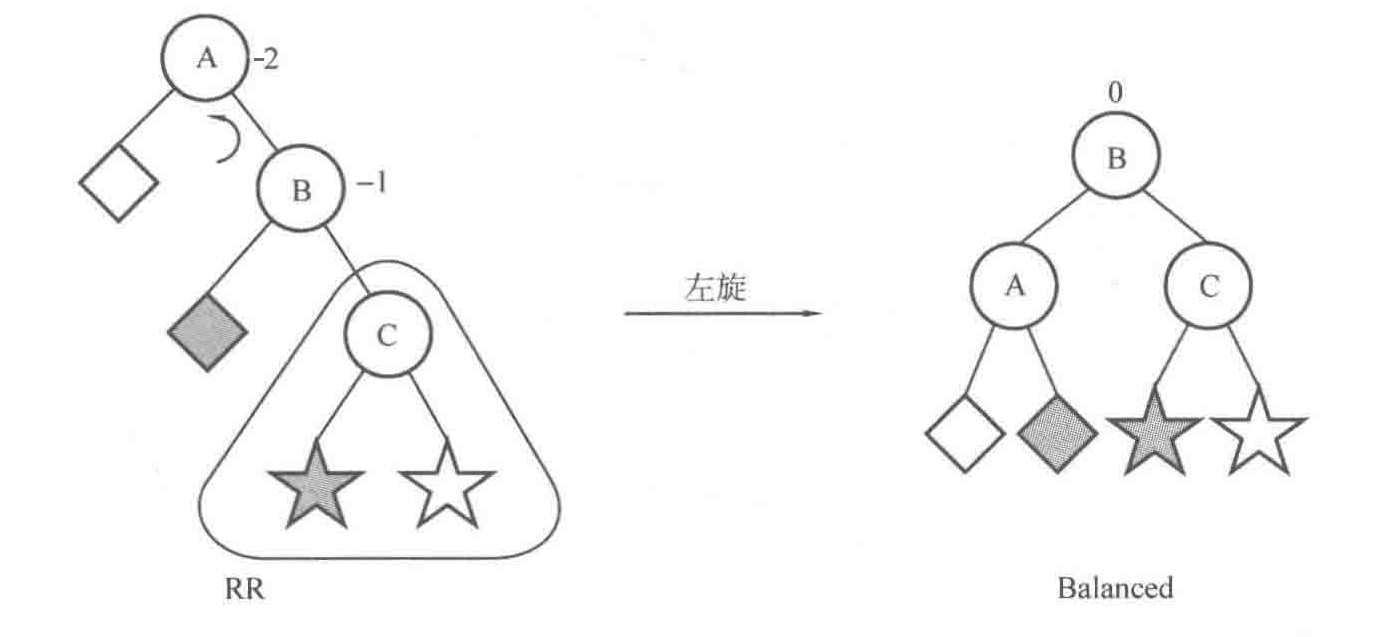
RR型的调整,只需要对平衡因子为-2的树使用左旋(L):
RL型的调整,先要对子树中平衡因子为1的右子树使用 右旋(R) 变成RR型,再对平衡因子为-2的结点使左旋(L) 即可:
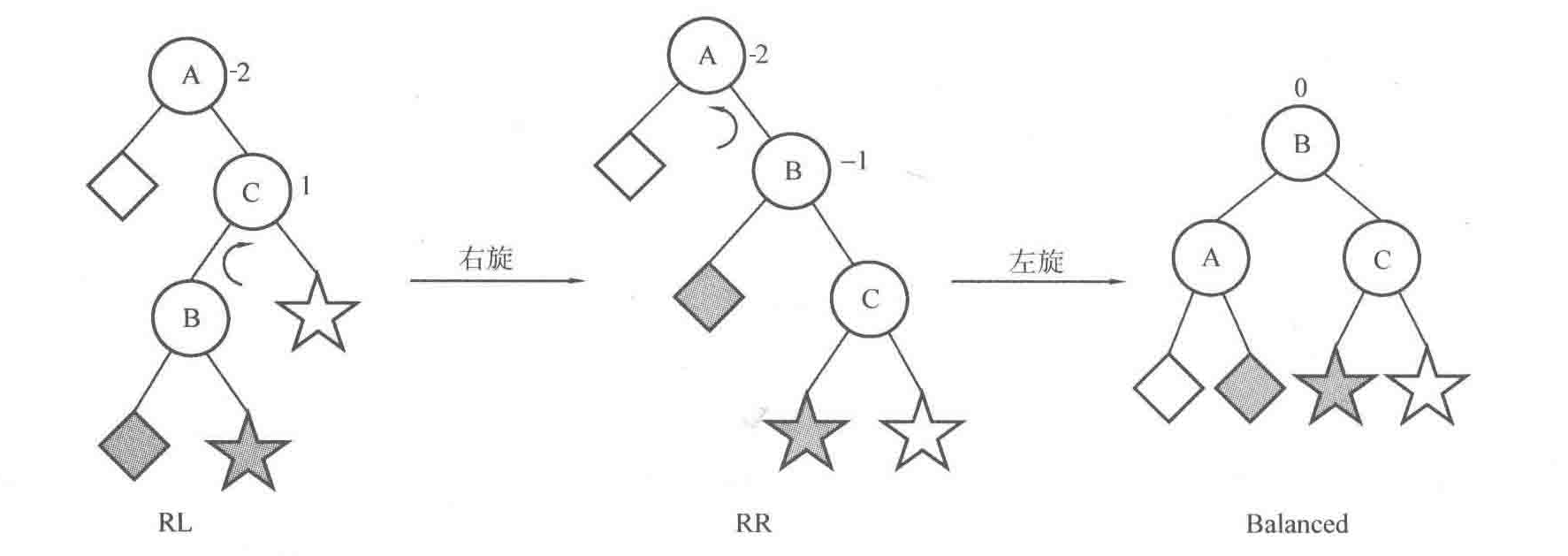
由上,可以得到平衡二叉树的插入算法,在插入的过程中,没插入一个结点,进行一次调整,算法代码如下:
void Insert(Node * &root,int x)
{
if(root==NULL){
root=newnode(x);
return;
}
if(x<root->data){ //插入到左子树
Insert(root->lchild,x);
updatehigh(root);
if(getbf(root)==2){
if(getbf(root->lchild)==1) //LL型
R(root);
else if(getbf(root->lchild)==-1){ //LR型
L(root->lchild);
R(root);
}
}
}
else{
Insert(root->rchild,x);
updatehigh(root);
if(getbf(root)==-2){
if(getbf(root->rchild)==-1) //RR型
L(root);
else if(getbf(root->rchild)==1){ //RL型
R(root->rchild);
L(root);
}
}
}
}小结,对不同树型的调整情况,作以下总结:
| 树型 | 判定条件 | 调整方法 |
|---|---|---|
| LL | BF(root)= 2,BF(root->lchild)= 1 | 对root进行右旋 |
| LR | BF(root)= 2,BF(root->lchild)=-1 | 先对root->lchild进行左旋,再对root进行右旋 |
| RR | BF(root)=-2,BF(root->rchild)=-1 | 对root进行左旋 |
| RL | BF(root)=-2,BF(root->rchild)= 1 | 先对root->rchild进行右旋,再对root进行左旋 |
平衡二叉树的建树
平衡二叉树的创建,类似于普通二叉树的插入方,只不过需要使用平衡二叉树专用的自动调整的插入方式,其代码如下:
//建立平衡二叉树
Node * CreatAVL(){
Node * root=NULL;
for(int i=0;i<n;i++){
int temp;
cin>>temp;
Insert(root,temp);
}
}









Comments | 3 条评论
*&是什么意思是啊呜呜呜,想半天想不懂
@Transrizo 就是一个指针类型变量的引用,通过这种方式,可以改变指针
@songjiahao 我要再仔细思考思考哈哈哈哈哈,谢谢