探究OpenGL中的坐标变换

　　OpenGL是非常强大而且广泛使用的3D图形API，其中坐标变换是一个至关重要的概念。本文将探究OpenGL坐标变换的基本原理，尤其是视图矩阵、投影矩阵的作用以及它们之间的关系，旨在记录和分享自己对OpenGL坐标变换的理解。

基础知识

　　理解OpenGL的坐标变换过程，需要一些基本的数学知识，包括但不限于向量、矩阵、线性代数和左右手坐标系等。你可以在其他任何地方找到非常优秀的数学知识讲解，比如LearnOpenGL教程的变换章节。因此，本文默认读者已经有了最基本的数学知识，至少学习到深究OpenGL坐标变换原理的读者一定有这些基本功了。

OpenGL的坐标系

　　OpenGL坐标变换中涉及以下几个坐标系：
　　1.局部坐标系：一个物体相对于自身的坐标系。用于描述物体内部的构成，如自身各个顶点的位置、法向量、切线等。
　　2.世界坐标系：用于描述整个三维场景的坐标系，所有一切物体都摆放在世界场景中。可以使用世界坐标系中的表示描述一个物体的位置、朝向等等。
　　3.相机坐标系：用于描述相机或者观察者位姿的坐标系，一般通过世界坐标系来定义或表示。在渲染过程中，一般将世界场景中的物体变换到相机坐标系中，经过裁剪后再映射到屏幕上。
　　4.裁剪坐标系：三维渲染中用于裁剪操作的坐标系，用于确定哪些物体或者图元要显示再屏幕上，即定义了一个由相机坐标系下某个可见空间范围归一化后的坐标系。
　　5.屏幕坐标系：用于在屏幕或者显示器上定位到一个像素的坐标系，也成为窗口坐标系。
　　引用LearnOpenGL中的图例，OpenGL坐标系的变换可以分为以下几个步骤：

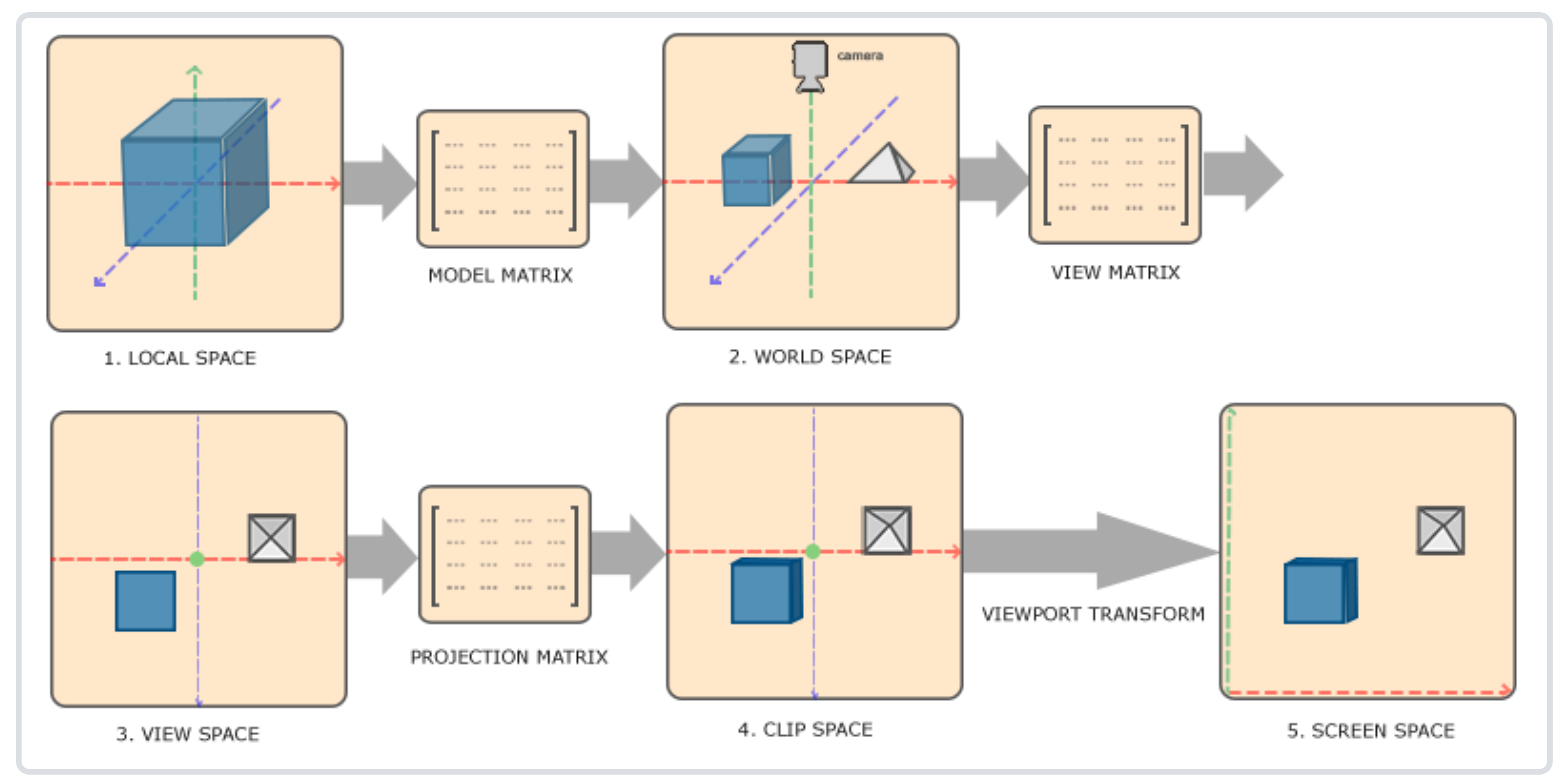
　　其中，从一个坐标系到另一个坐标系的变换都通过一个矩阵实现，学习和使用OpenGL过程中常用到的三个矩阵的功能如下：
　　1.模型矩阵：将物体的坐标从局部坐标系转换到世界坐标系。模型矩阵决定了物体在世界坐标系中位置、方向和大小。
　　2.视图矩阵：将物体的坐标从世界坐标系转换到相机坐标系。视图矩阵决定了在观察者的角度看到的物体位置和姿态，本质上还是从一个坐标系到另一个坐标系的变换。
　　3.投影矩阵：将物体的坐标从相机坐标系转换到裁剪坐标系。在OpenGL中，投影矩阵由两个主要的功能：确定了可视范围，归一化到裁剪坐标系。根据投影方式，OpenGL中的投影矩阵又分为正交投影和透视投影。
　　到此，我们大致说明了坐标系变换的流程及各个变换矩阵的作用。

模型矩阵

　　模型矩阵将物体从局部坐标系变换到世界坐标系中，是一个4*4的矩阵，模型矩阵可以执行平移、旋转和缩放等变换操作。通过组合多种平移、旋转和缩放变换，可以构建复杂的模型矩阵，描述物体到世界坐标系中的变换。模型矩阵最好理解，此处不再展开阐述，将重点放在视图矩阵和投影矩阵上。

视图矩阵

　　视图矩阵将物体从世界坐标系中转换到相机所在的坐标系。我认为在OpenGL的大多数教程中，对视图矩阵的讲解要么一笔带过，要么生涩难懂。本文中将以坐标系转换基本原理的角度，以两种方式来解释视图矩阵的来由。

坐标变换的实质

　　为了阐明视图矩阵的变换原理，我们需要重点理解坐标变换的实质：
　　1.三维坐标系中两个向量点积的含义是什么？
　　两个向量的点积表示两个向量长度的乘积乘以两个向量之间夹角的余弦值，计算方法为：

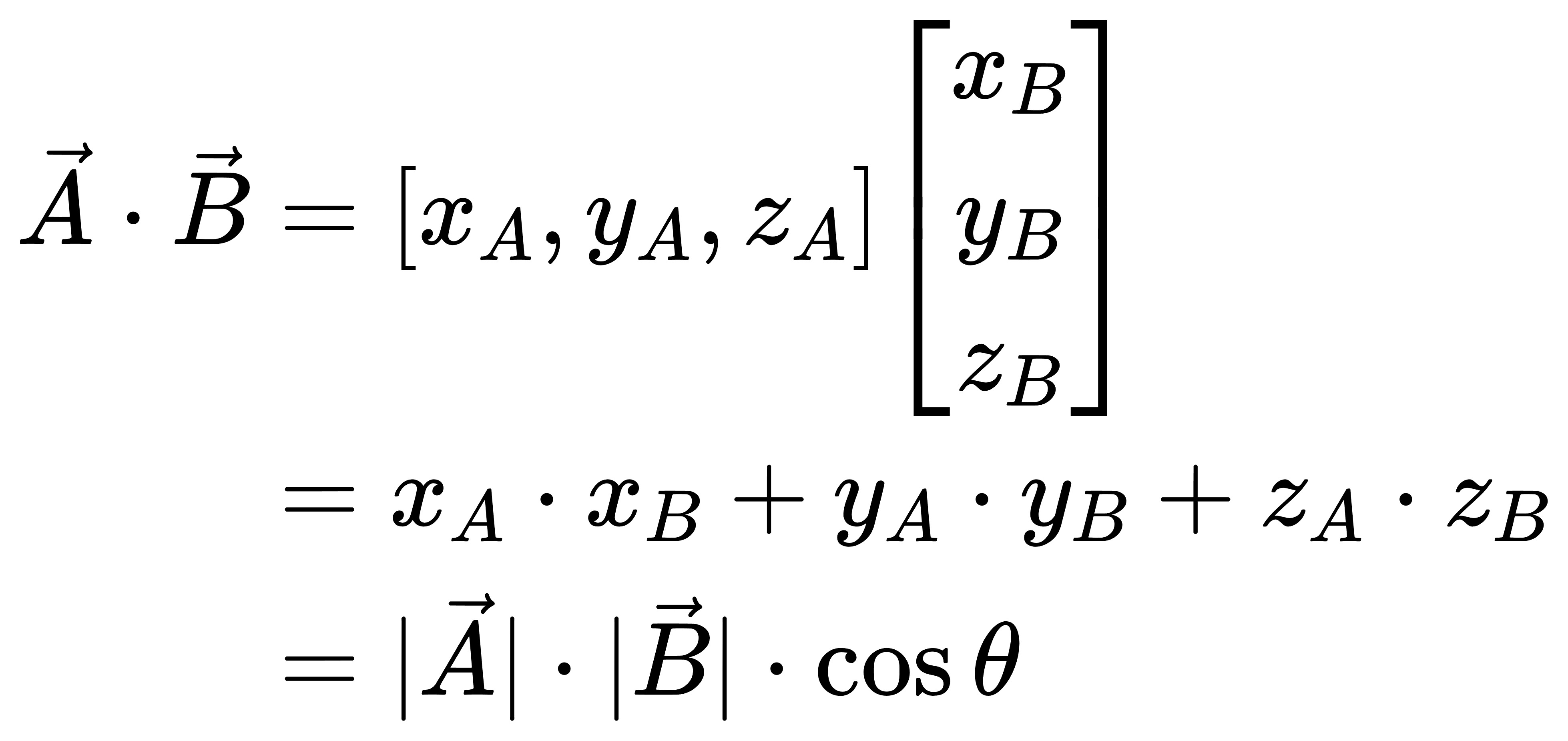
　　对于上述公式中点乘的向量A和向量B，如果向量A是一个单位向量，那么最终的计算结果即为向量B在向量A方向上的投影长度。
　　2.三维坐标系中一个顶点是如何表示的？

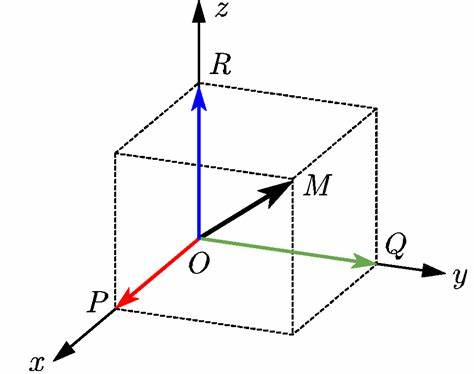
　　如上图所示，我们从正反两个角度去理解一个顶点在坐标系统中的表示：
　　（1）对于点M，在三维坐标系中的点坐标其实是从原点O到点M的向量OM在三个坐标轴上的投影长度构成的，即：

　　（2）将点M的坐标表示为(xm,ym,zm)，向量OM则可以表示为将X、Y、Z轴的单位向量（一组单位正交基）按照(xm,ym,zm)进行线性组合得到，即：

　　3.坐标系变换的实质是什么？
　　当我们能够理解点在一组单位正交基中的表示方法以后，我们不难发现一个事实：坐标系变换的实质是使用另一组单位正交基表示三维空间中的点。

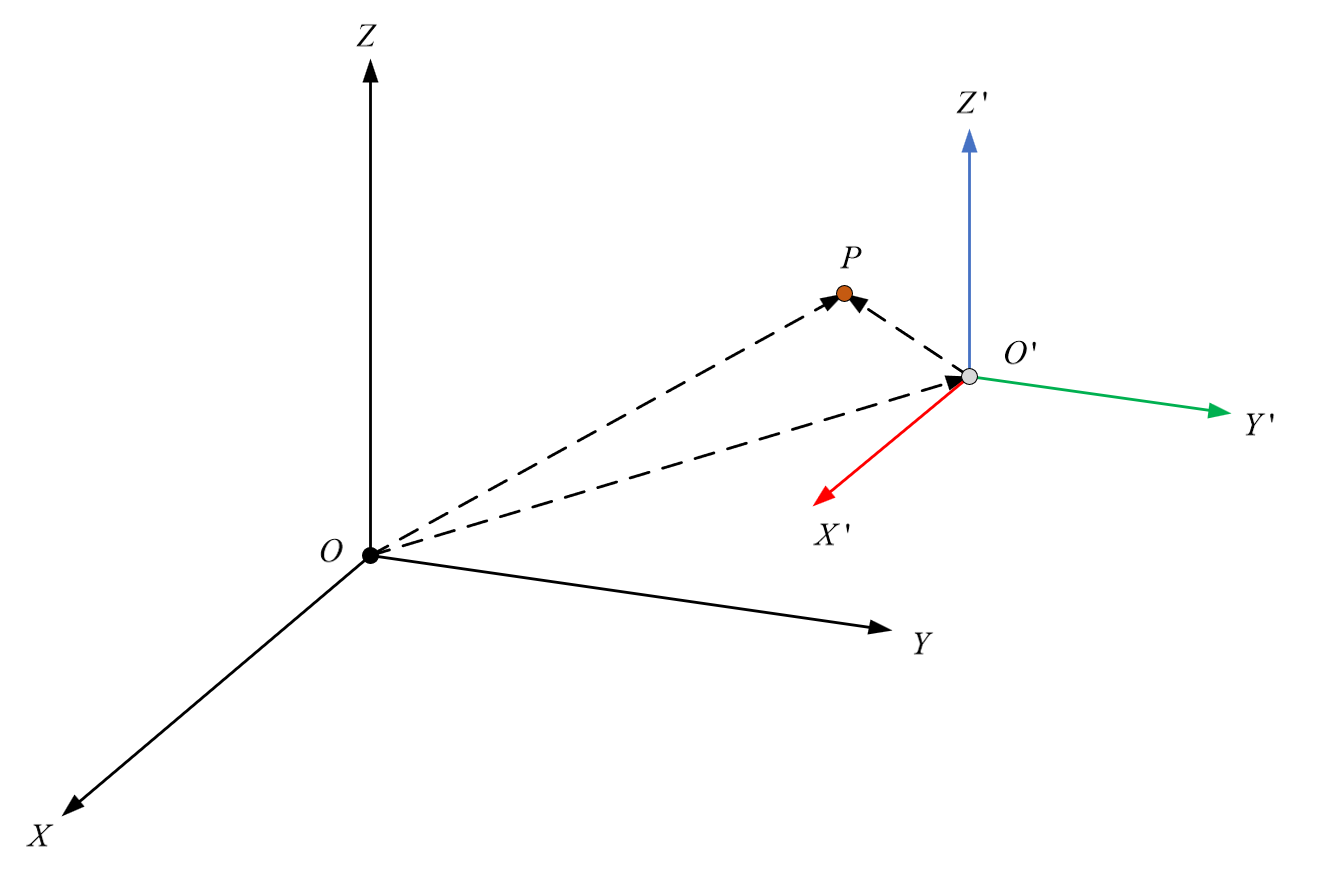
　　以上图为例，将X-Y-Z坐标系中的点P变换到X'-Y'-Z'的新坐标系中，其实相当于在新的坐标系中表示P。
　　接下来，我们来推导P点从X-Y-Z坐标系变换到X'-Y'-Z'坐标系的计算过程：
　　（1）以2.(1)中表述的表示方法考虑P点在新坐标系中的表示：
　　如果记点P在X-Y-Z坐标系的坐标为(x,y,z)，在X'-Y'-Z'坐标系中的坐标为(x',y',z')，记点O'在X-Y-Z中的坐标为(xo',yo',yo')。那么，(x',y',z')就可以表示为O'P在X'、Y'、Z'上的投影。如下所示：

　　如果将这个变换过程扩展到齐次坐标中，公式就会有些许的变化：

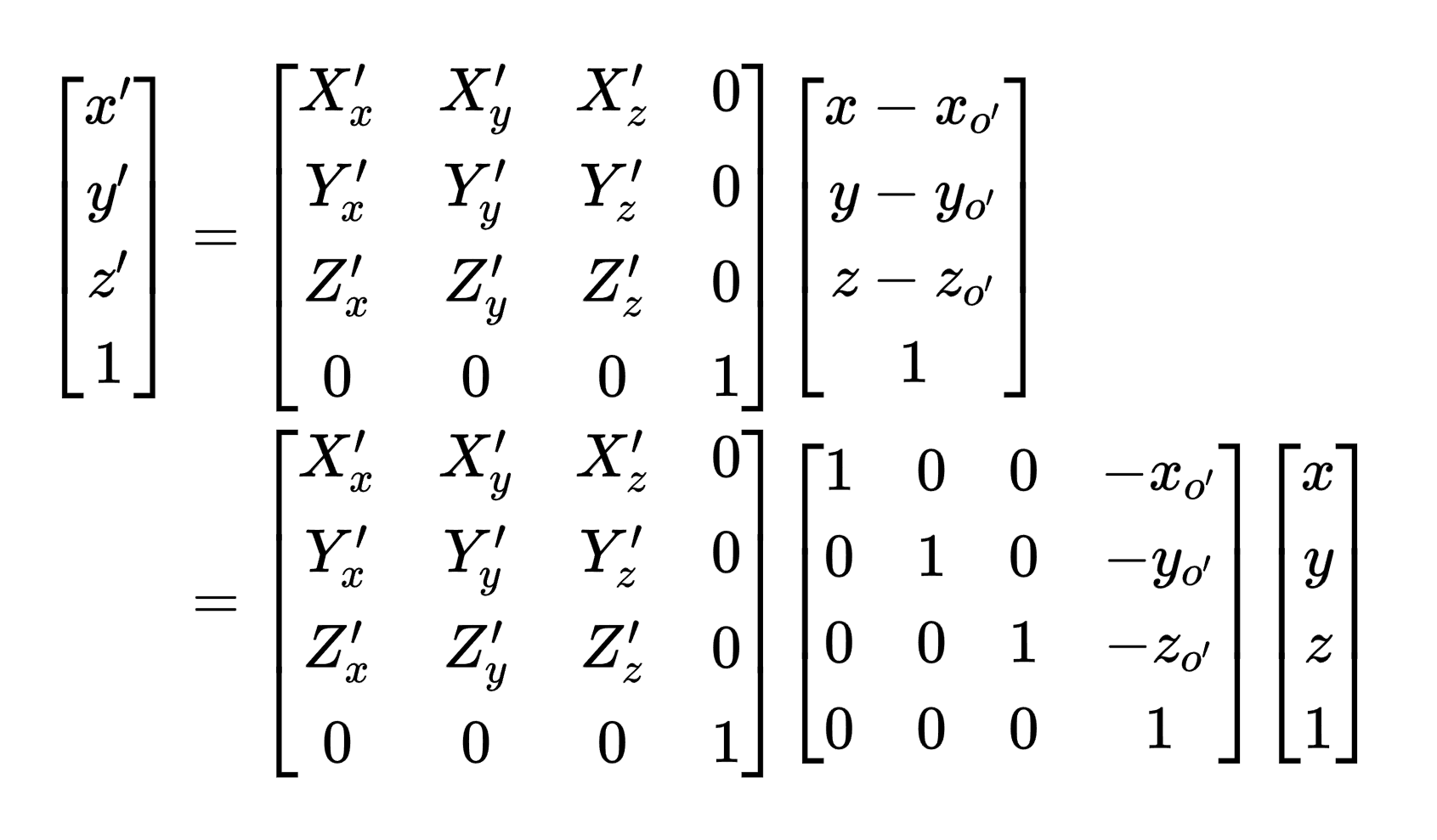
　　看过LearnOpenGL的小伙伴可能会发现这个变换矩阵是如此得眼熟，没错这就是LookAt矩阵的计算原理。
　　（2）再以2.(2)中表示的方法思考P点再新坐标系中的坐标的计算方法：
　　上一个方法中，我们通过坐标的本质含义正向求得P点在心坐标系中的坐标。根据2.(2)中的思想，向量OP可以通过原坐标系X、Y、Z轴上的单位向量线性组合得到，O'P可以通过新坐标系中X'、Y'、Z'轴上的单位向量线性组合得到，且有OO'+O'P=OP。向量OP的线性组合系数即为其坐标(x,y,z)，记向量O'P由X'、Y'、Z'轴构成的单位正交基线性组合的系数为(x',y',z')。那么我们可以得到以下的方程组：

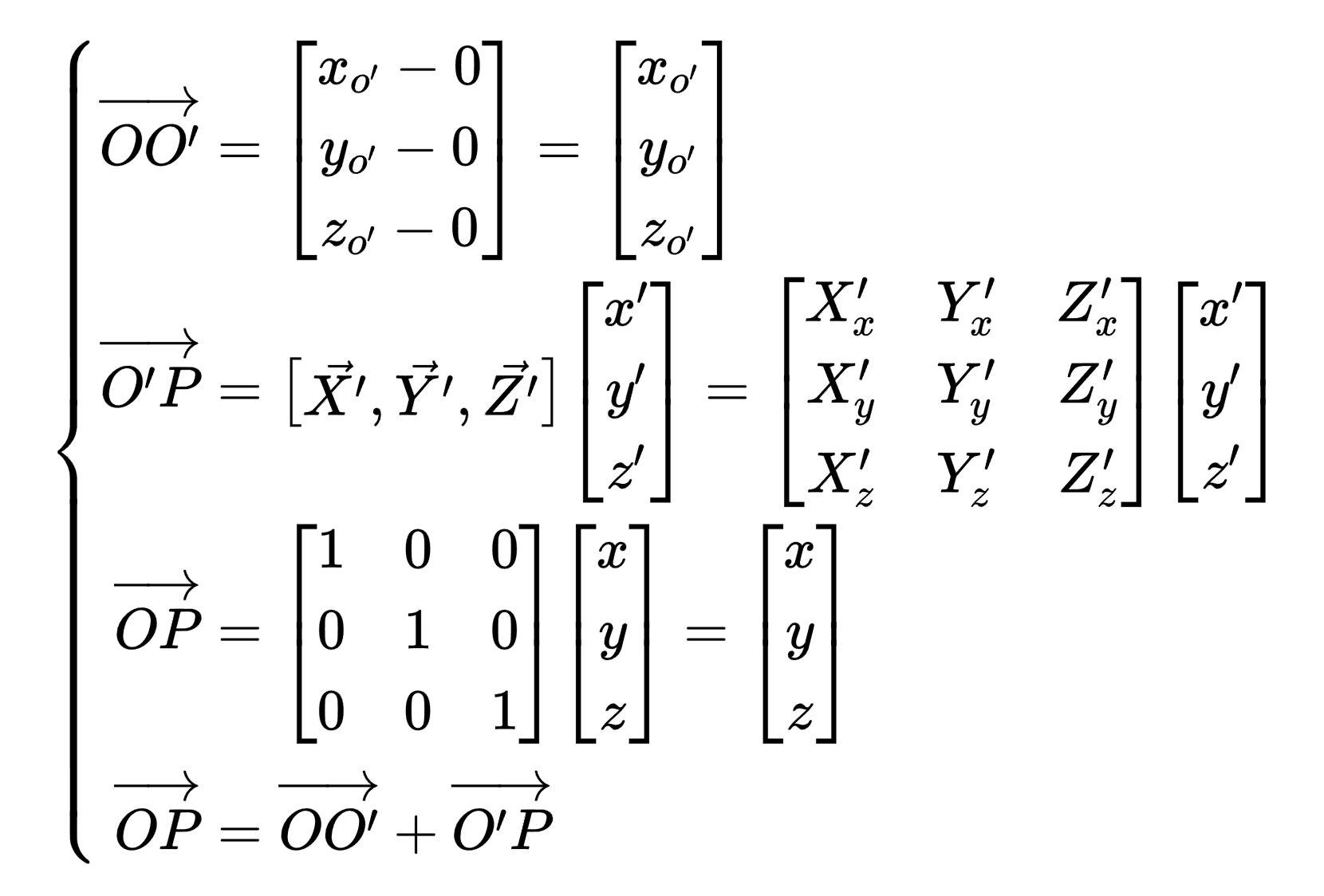
　　对方程组进行求解，得到(x',y',z')的表达如下：

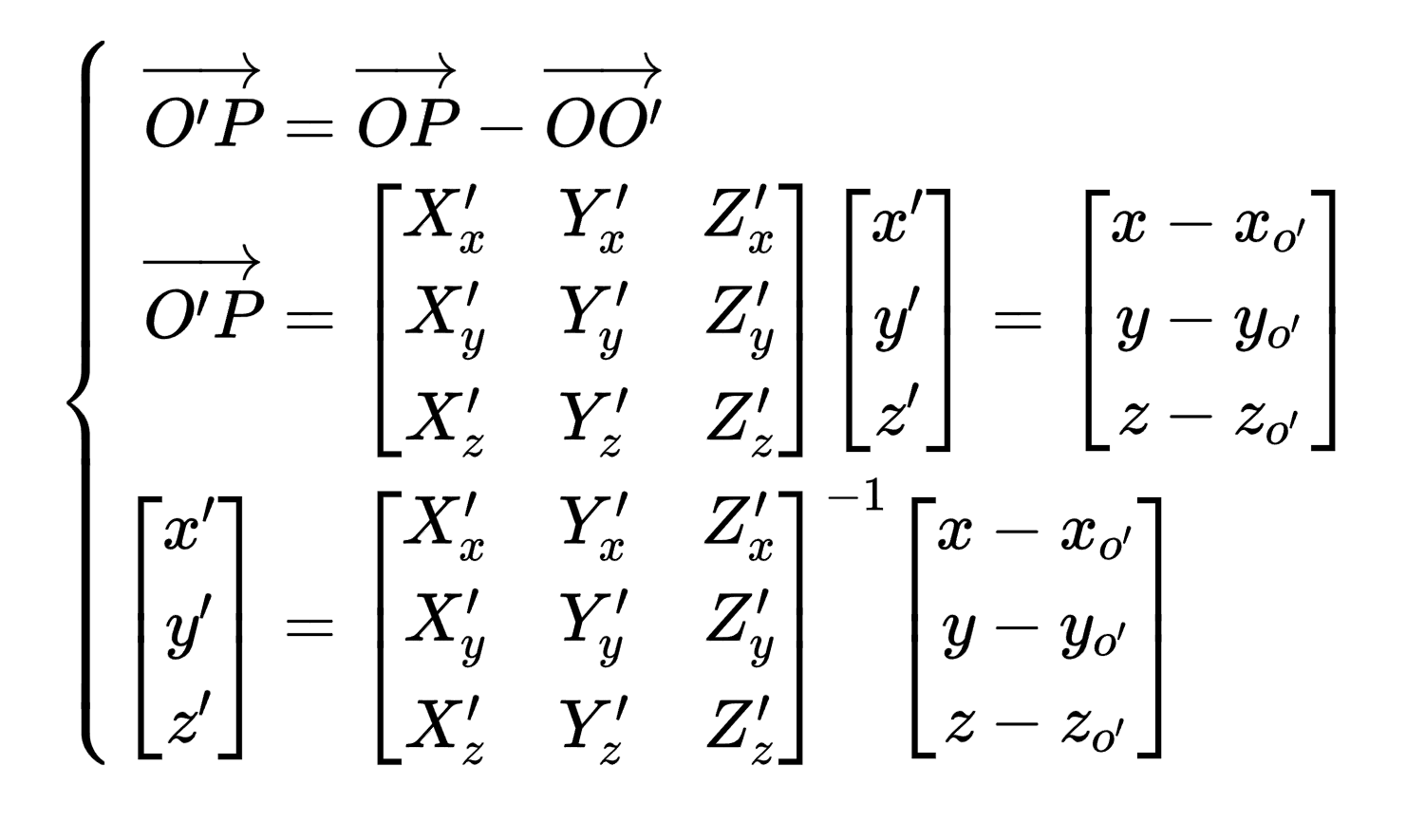
　　根据线性代数的知识，正交矩阵的逆矩阵等于其转置矩阵，进一步可以得到：

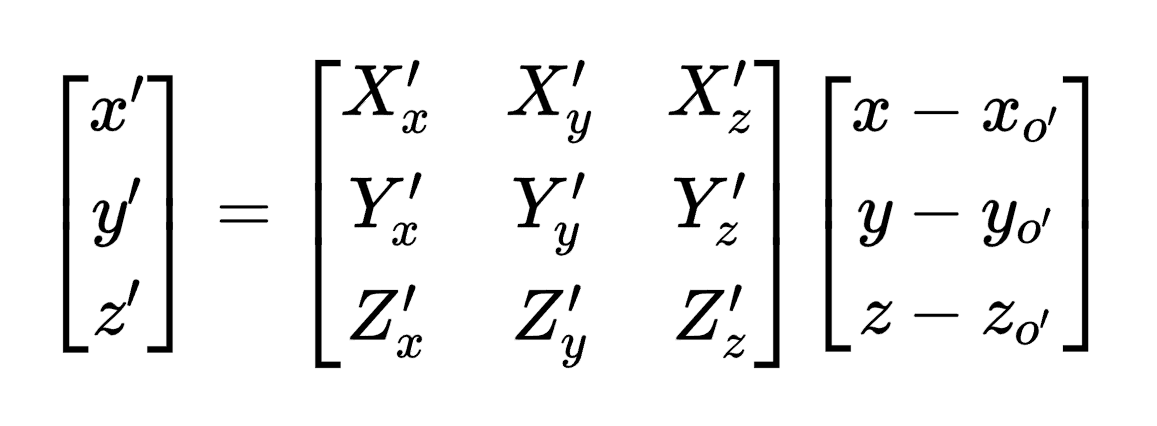
　　殊途同归，解释的角度不同，但是本质是一样的，因此得到的变换矩阵也是一样的。将其扩展到齐次坐标中就能得到最终完全一致的结果。至此，本文就已经完整的解释了坐标变换的实质。
　　不得不说的是，LearnOpenGL的教程中直接了当地给出了这个矩阵的表示，虽然并没有展开讲解，但是直接了当，标注清晰。其他某些教程或者讲解中，将上述变换过程分解为相机移动到原点和旋转变换这样看似生动但是让人摸不着头脑的解释实在让人难以接受！

OpenGL中的视图矩阵

　　有了上述讲解，对于视图变换矩阵的过程，应该就非常好理解了。本质上来说，就是将世界坐标系中的点变换到视图坐标系下进行表示。对于使用OpenGL的人而言，我们需要做的就是定义好相机坐标系的X-Y-Z轴。

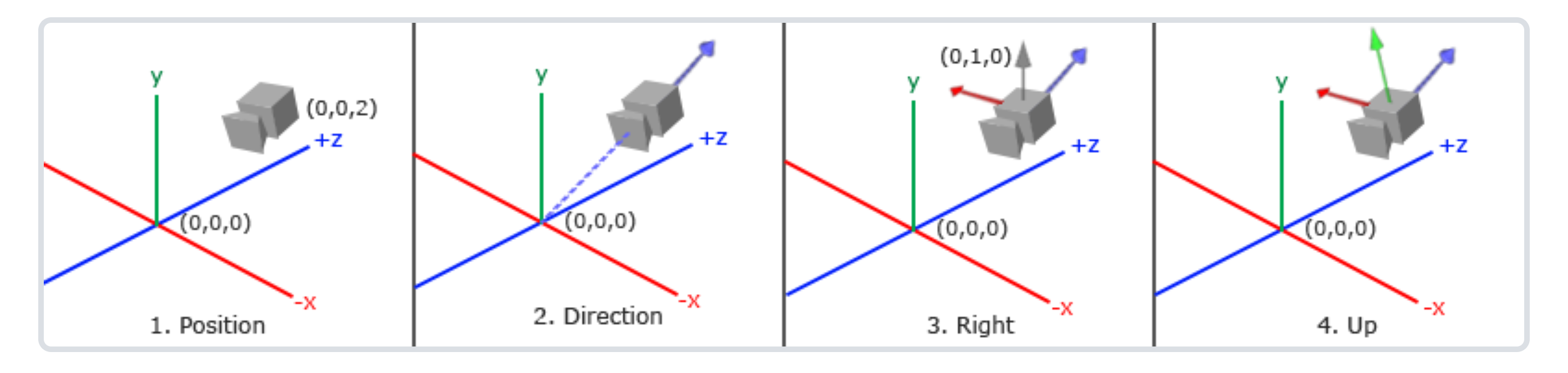
　　如上图所示，在OpenGL中指定相机坐标系中X轴为相机的右方向，Y轴为相机的上方向，Z轴为相机看向的反方向。至于为什么这么规定，我认为相机要往反方向运动之类的解释并不能让人信服。个人的理解倾向于，坐标系中采用的轴向最终还是服务于后续的投影变换（比如：考虑到方便后续的计算）。
　　如果我们按照LearnOpenGL中的记法：P表示相机所在的位置，R表示相机的右方向（X轴），U表示相机的上方向（Y轴），D表示相机的位置方向（即相机看向的反方向，Z轴）。将其带入上一小节的推导公式中，我们就可以得到和LearnOpenGL中一样的LookAt矩阵表示：

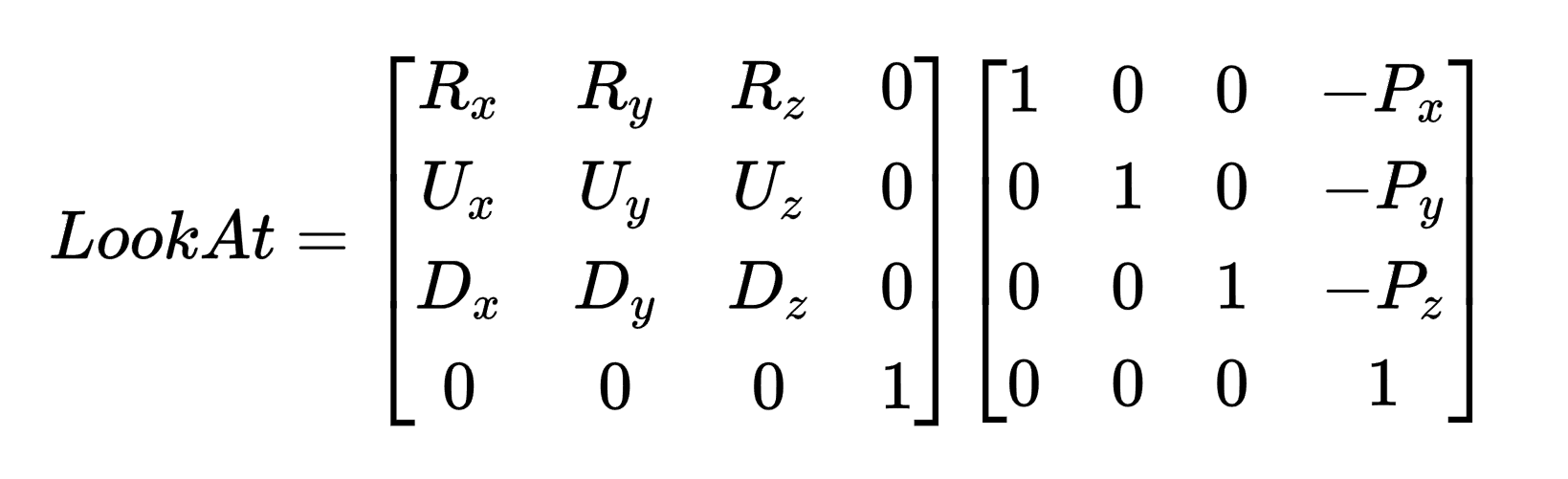
　　这里需要留意一个细节：在相机视野内的所有物体变换到相机坐标以后，其坐标的z分量都是负值（在投影矩阵运算时将会有所影响）。
　　紧接着，我们通过glm数学库中LookAt矩阵在计算OpenGL中视图矩阵的代码来分析：

template<typename T, qualifier Q>
GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAtRH(vec<3, T, Q> const& eye, vec<3, T, Q> const& center, vec<3, T, Q> const& up)
{
    vec<3, T, Q> const f(normalize(center - eye));
    vec<3, T, Q> const s(normalize(cross(f, up)));
    vec<3, T, Q> const u(cross(s, f));

    mat<4, 4, T, Q> Result(1);
    Result[0][0] = s.x;
    Result[1][0] = s.y;
    Result[2][0] = s.z;
    Result[0][1] = u.x;
    Result[1][1] = u.y;
    Result[2][1] = u.z;
    Result[0][2] =-f.x;
    Result[1][2] =-f.y;
    Result[2][2] =-f.z;
    Result[3][0] =-dot(s, eye);
    Result[3][1] =-dot(u, eye);
    Result[3][2] = dot(f, eye);
    return Result;
}

　　glm数学库中在计算得到三个轴向的单位向量后直接带入我们推导的公式进行了计算，结果如下：

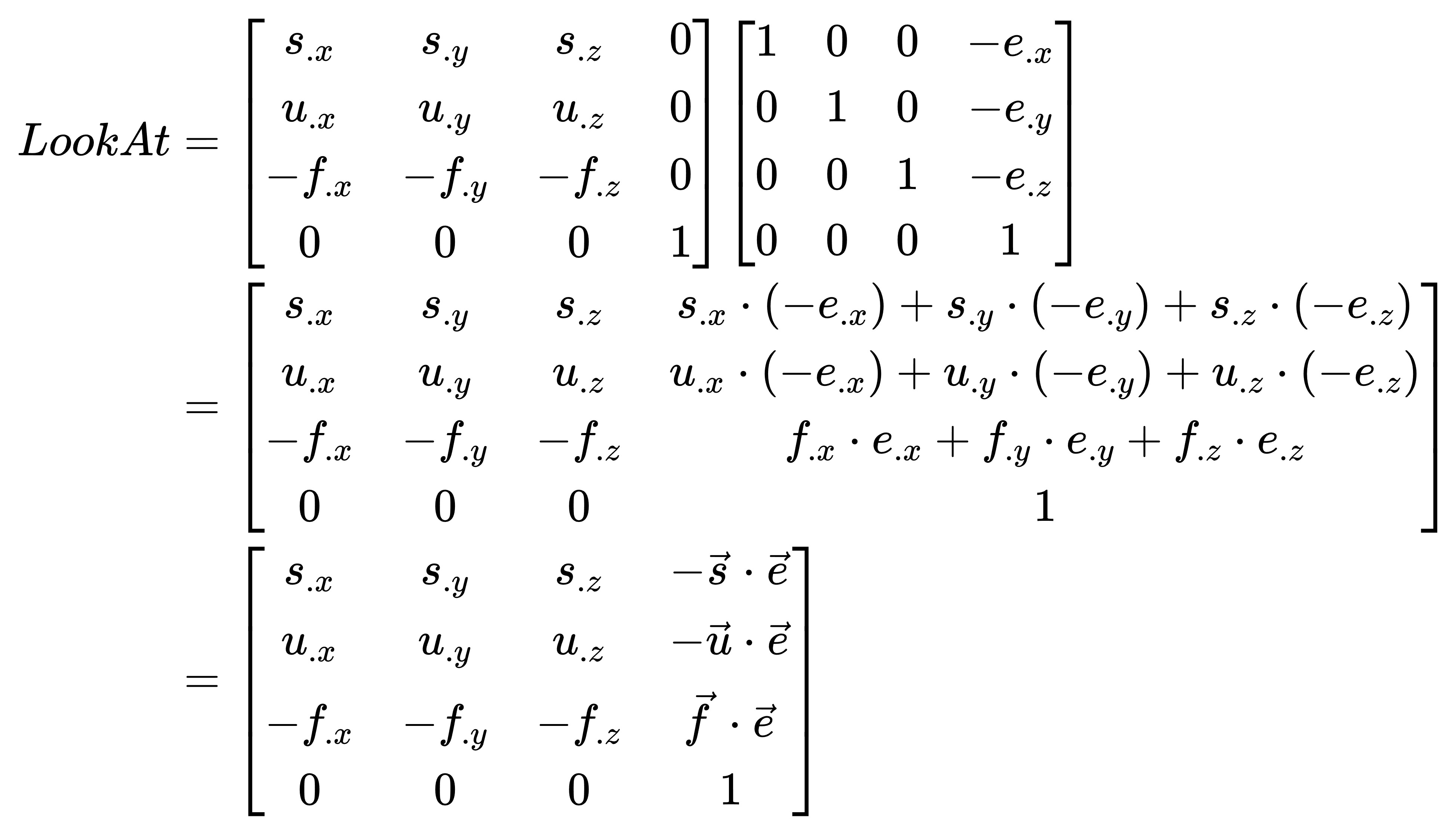
　　计算得到的结果和glm库中的运算完全一致（glm库中的矩阵是列优先的，因此看起来像是转置了一下）。

投影矩阵

　　投影矩阵的作用是规定一个坐标范围，并将这个范围内的坐标归一化映射到标准设备坐标系范围内。这意味着，不在规定的范围内的坐标将会被抛弃，而在规定范围内的坐标需要通过一定的计算方法将转换到标准化设备坐标系（NDC，Normalized Device Coordinates）中（在OpenGL中标准化设备坐标系是一个三个维度从-1.0~1.0的立方体，且采用左手系——X轴朝右，Y轴朝上，Z轴朝屏内）。
　　根据投影方法的不同，投影矩阵又分为正交投影和透视投影。

正交投影

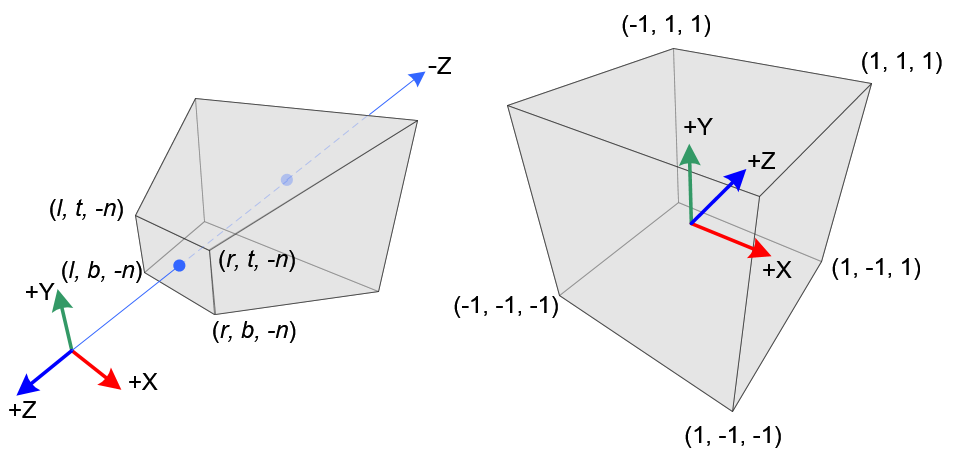
　　正交投影变换限定的范围是一个长方体区域。从相机的角度看去，这个区域通过左右边界，下上边界，近平面-远平面来限制，最终转换到NDC坐标系中，如下图所示：

　　根据图示，我们可以看到最终将X轴上[left,right]，Y轴上[bottom,top]，Z轴上[-near,-far]空间上的坐标分别映射到NDC三个轴上[-1.0,1.0]范围内。这里必须说明一点，在使用glm数学库创建一个正交投影矩阵时，给定的近平面near和远平面far参数都是正值，而我们上一节讲到OpenGL中的view变换使得在相机可视范围内的点z分量都是负值，故glm数学库在实现时则是将Z轴上[-near,-far]区间映射到[-1.0,1.0]。接下来，我们一起分析正交投影变换矩阵的计算方法：
　　对于X轴和Y轴上来说，计算方法时一致的，Z轴上由于从相机坐标系的右手系变为NDC的左手系处理起来有些许区别。对于一个顶点的坐标来说，xyz三个分量是分开计算的。
　　先以x分量举例说明：

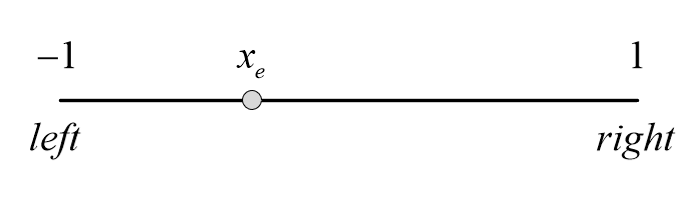
　　如图所示，视图坐标系下的xe映射到[-1.0,1.0]区间内，从几何的角度可以考虑如下的计算，-1表示目标区间的左边界，2表示目标区间的长度，分式表示了xe到left的距离占left~right整个区间的长度比例：

　　y分量的计算和x分量完全一样，而z分量正如之前所说是将Z轴上[-near,-far]映射到[-1.0,1.0]，则计算过程变为：

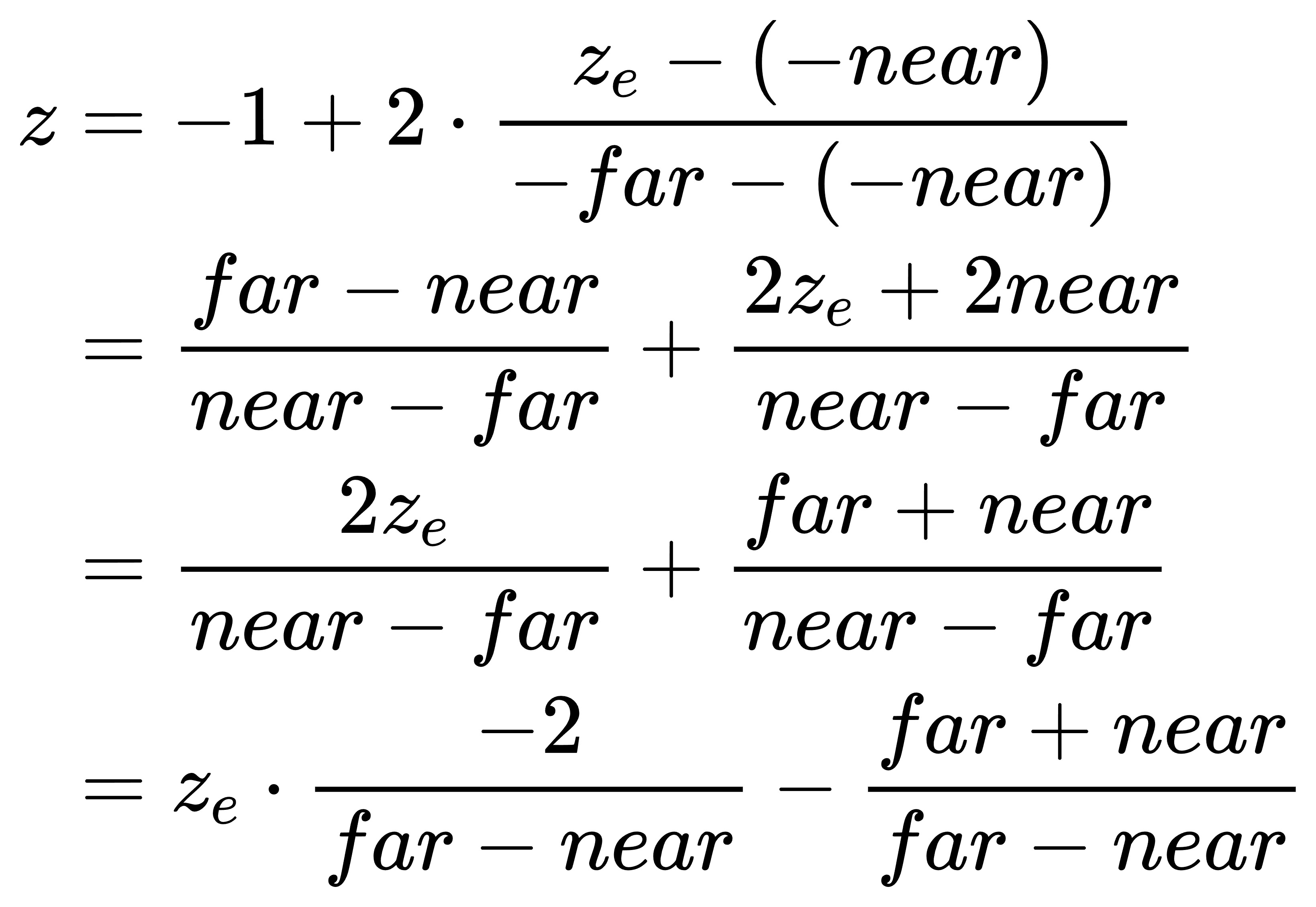
　　那么，最终的正交投影变换矩阵的齐次形式可以写为：

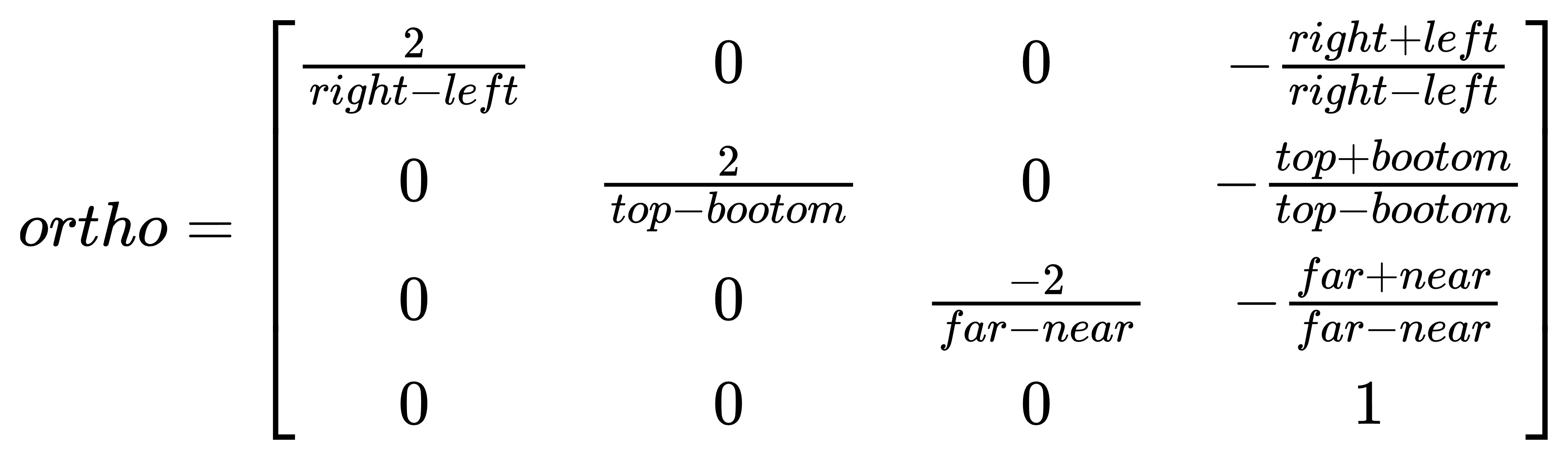
　　同样的，glm数学库中对于正交投影矩阵的实现与分析一致（glm库中的矩阵是列优先）：

template<typename T>
GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> orthoRH_NO(T left, T right, T bottom, T top, T zNear, T zFar)
{
    mat<4, 4, T, defaultp> Result(1);
    Result[0][0] = static_cast<T>(2) / (right - left);
    Result[1][1] = static_cast<T>(2) / (top - bottom);
    Result[2][2] = - static_cast<T>(2) / (zFar - zNear);
    Result[3][0] = - (right + left) / (right - left);
    Result[3][1] = - (top + bottom) / (top - bottom);
    Result[3][2] = - (zFar + zNear) / (zFar - zNear);
    return Result;
}

透视投影

　　透视投影变换限定的范围是一个视锥体。从功能上看原理和正交投影类似，不过计算方法有所区别，增加了透视除法的变换。下图展示了从透视投影的视锥体到NDC坐标系的转换关系：

　　透视投影在转换坐标系时，需要考虑透视关系。同样地，由于OpenGL中的view变换使得在相机可视范围内的点z分量都是负半轴上（负值）透视投影的的Z范围也是[-near,-far]区间。参考Songho文章中的计算过程并结合自己的理解，本文将透视投影的计算过程整理如下：
　　透视投影的转换过程可以进一步拆解为两个步骤：先透视变换，再归一化到NDC坐标系中。
　　首先，透视关系会将所有的视锥体中的所有物体投影到近平面的范围内，以保证近大远小的效果，如下图所示：

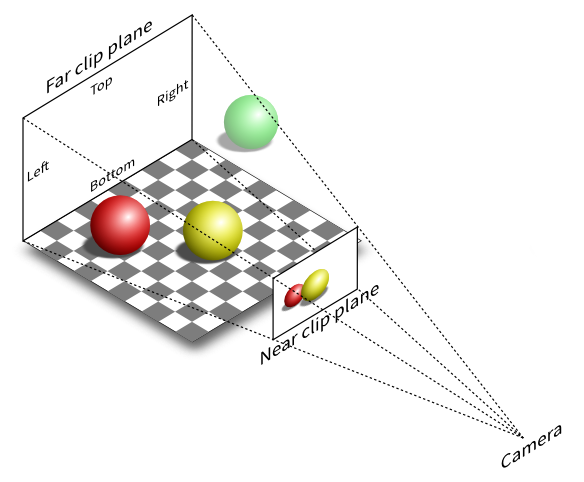
　　不难看出，物体大小的显示效果是由X-Y轴上的坐标控制的。这意味着在变换的计算过程中，物体的远近（z坐标分量）会对x和y坐标的变换产生产生影响（z坐标分量对x和y坐标分量的计算影响其实是一致的）。上图展示了俯视视角和侧视视角下的透视关系:

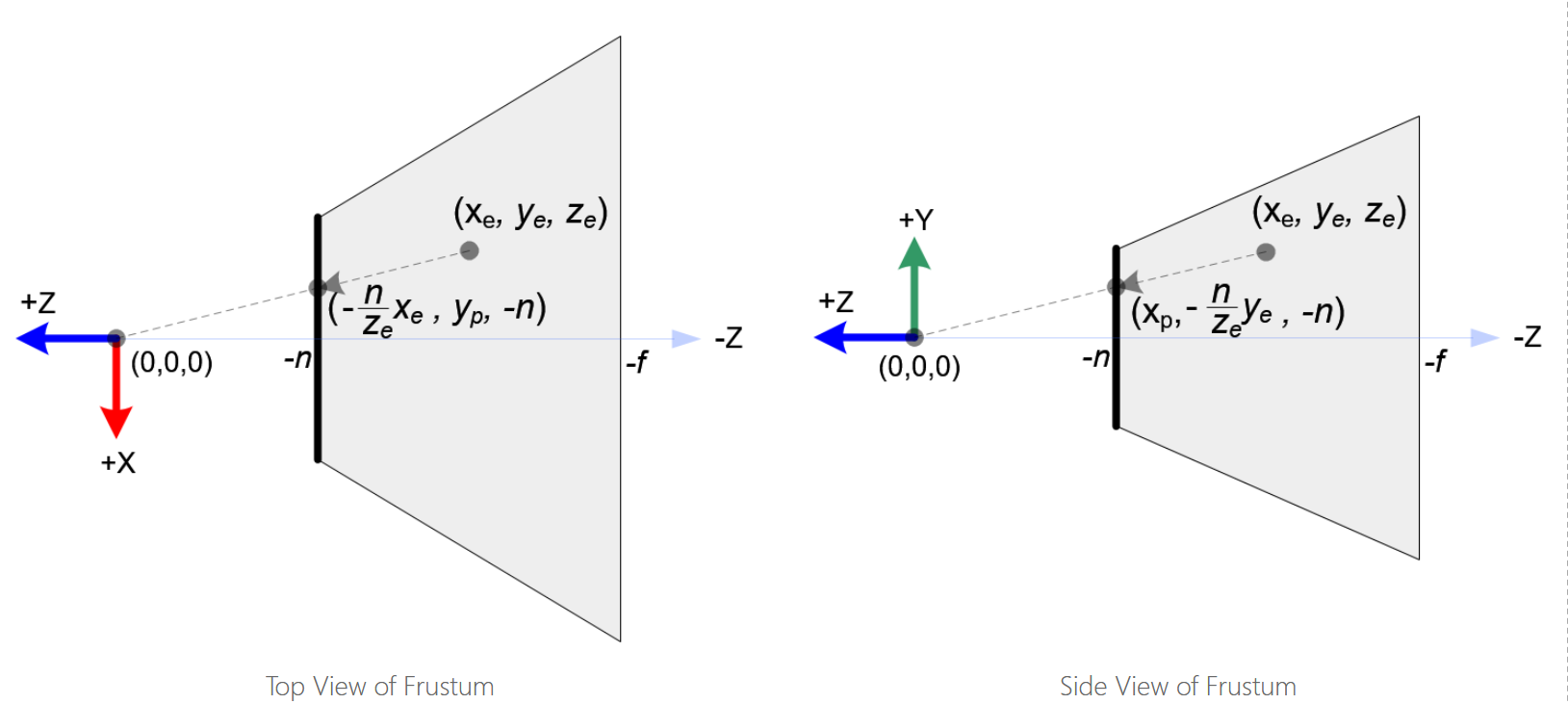
　　这里以x坐标的计算过程为例介绍透视关系的变换方法:

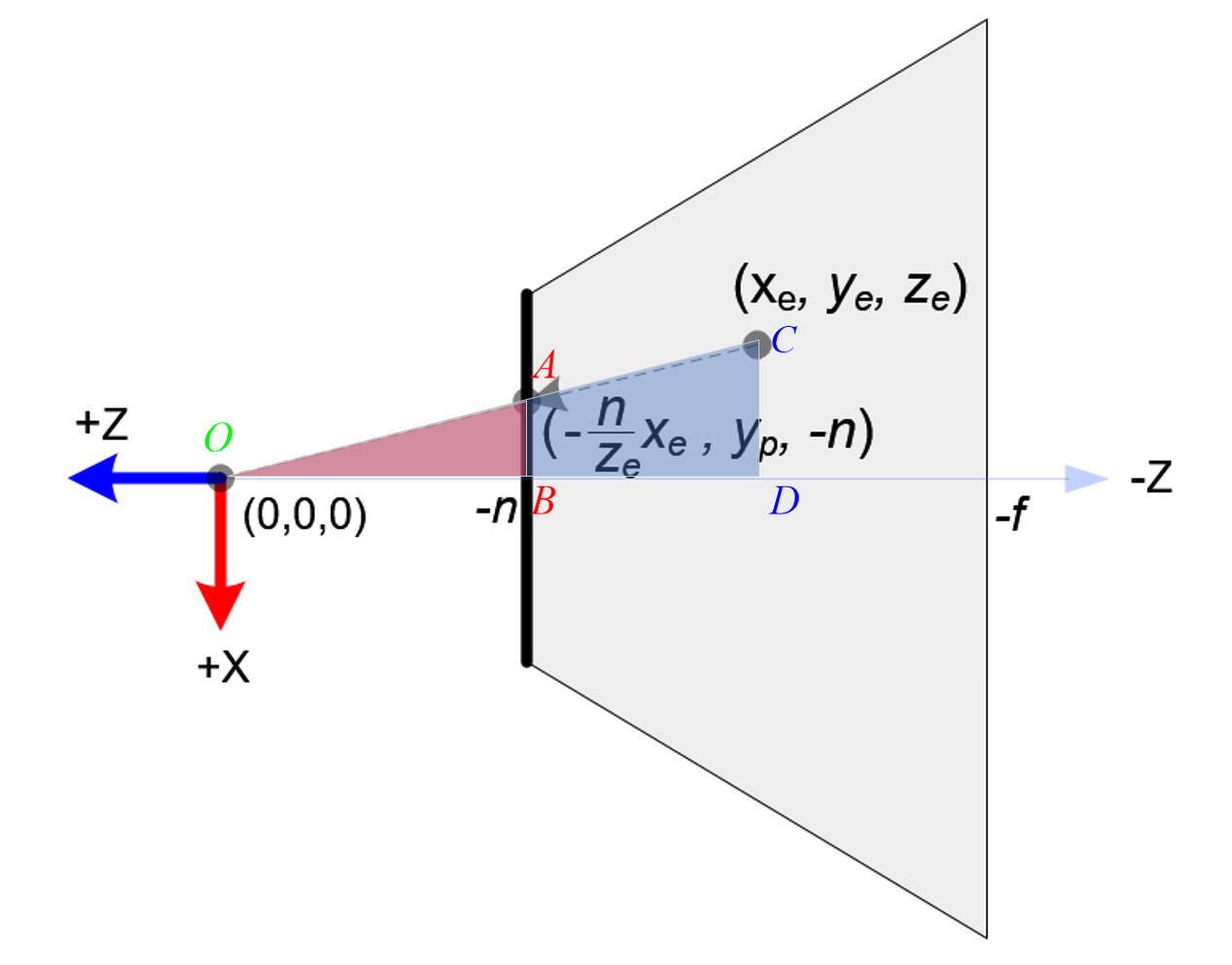
　　视图坐标系中有一个点P(Xe, Ye, Ze)，通过透视关系（P点和相机位置连线在近平面上交点的x-y坐标即为投影的后的大小，这么解释比较怪异的是其实并没有真的将P点投在近平面上，因为z分量是不受透视影响的，仅仅影响x-y坐标的计算而已。）可以看到三角形OAB和三角形OCD是相似三角形。通过这一几何关系，我们可以得到一组等比关系：

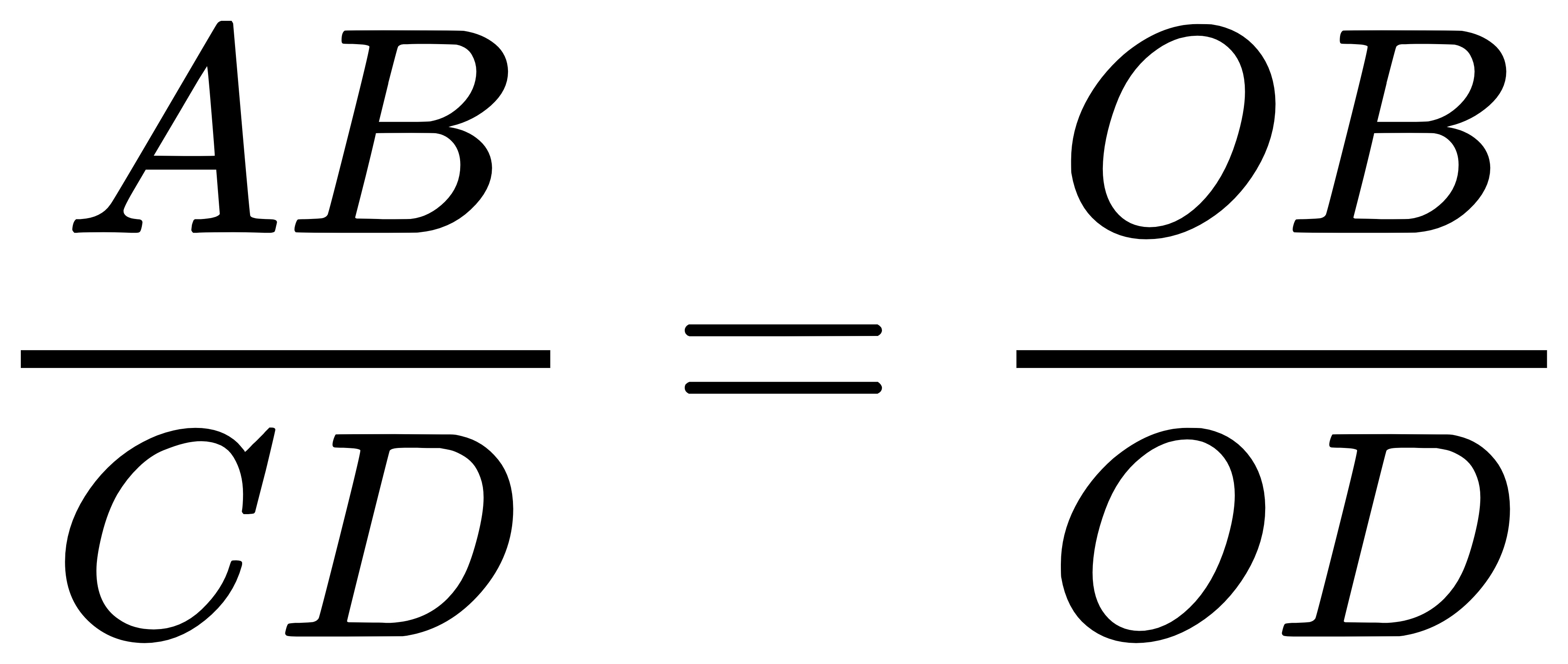
　　使用坐标表示为：

　　经过简单的变换便可以得到透视变换后的x坐标：

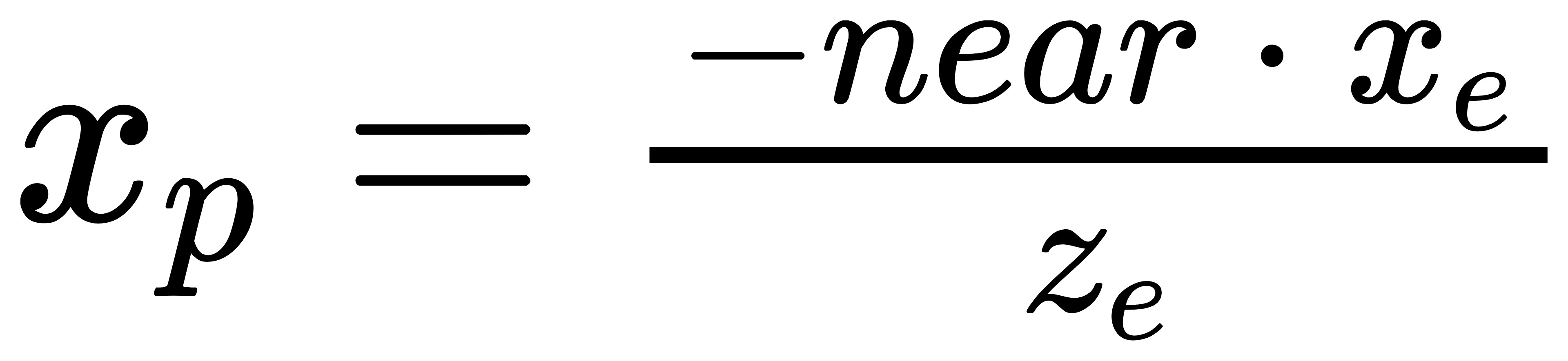
　　然后，我们再对透视变换后的坐标归一化到NDC坐标系下，归一化的过程和正交变换类似了，也就是将透视变换后的坐标映射到[-1.0,1.0]区间。根据正交投影变换中映射的计算公式可以直接得出：

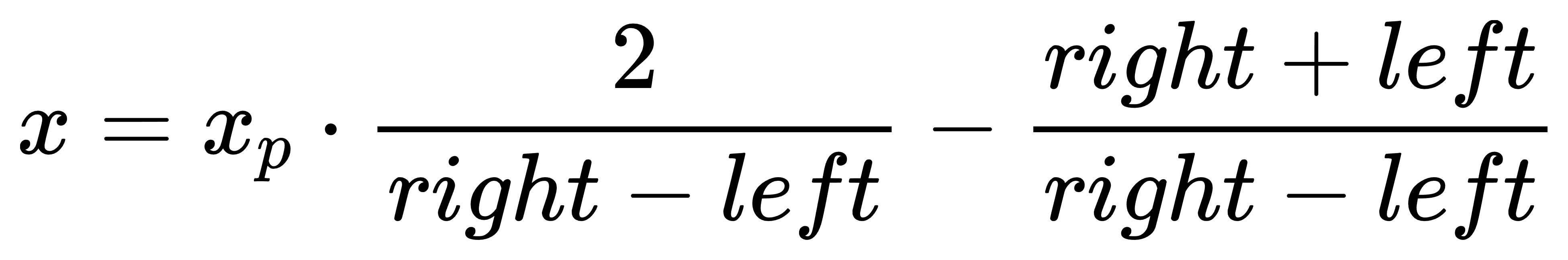
　　联立上面透视变换和归一化的两个公式可以得到：

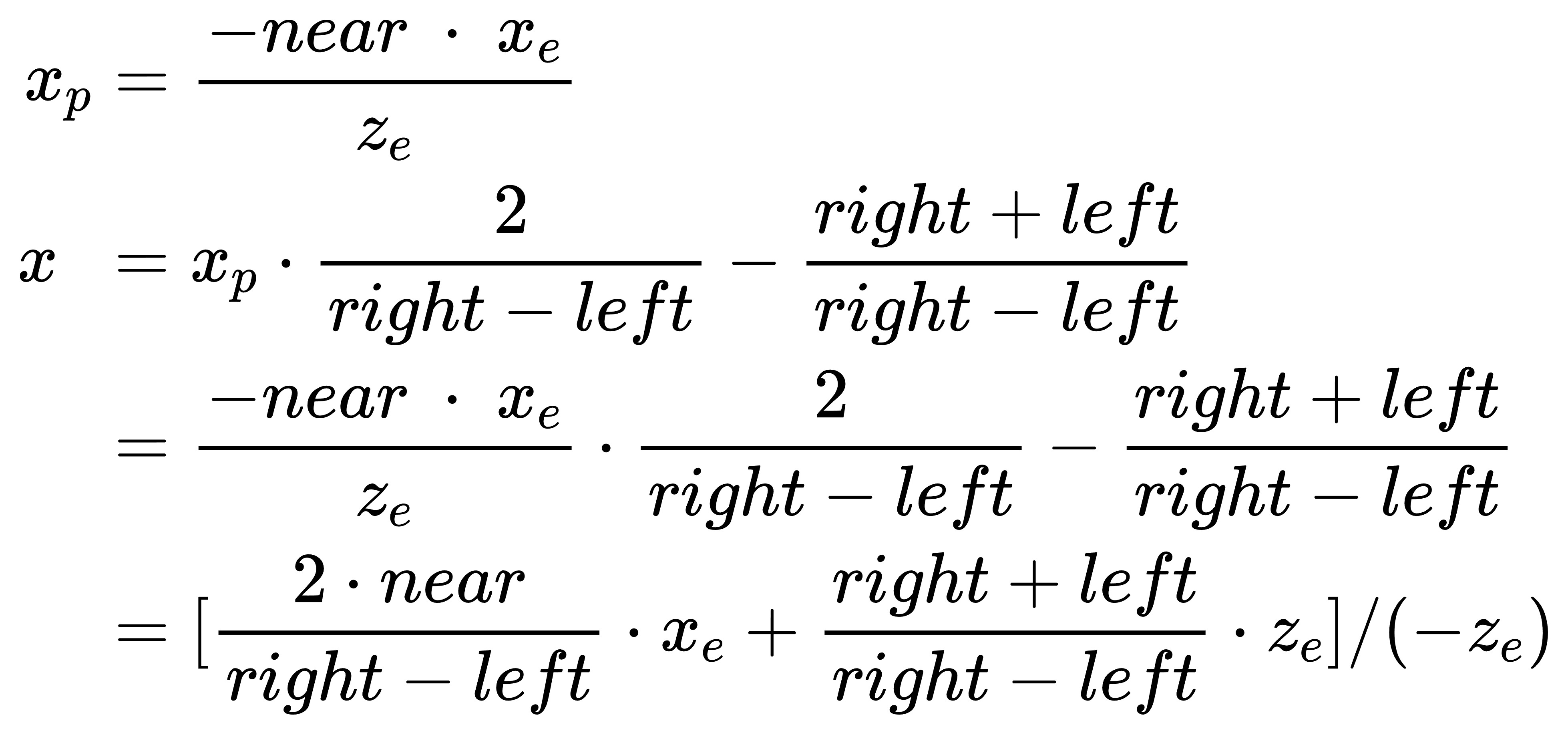
　　y坐标的变换计算和x计算方式一致。同理，我们可以得到y坐标的变换计算公式：

　　很重要的一点：OpenGL中的gl_Position其实是齐次坐标表示的，即有四个分量，x-y-z分量最终都会除以w分量。观察上述式子中x坐标和y坐标的表示方法，我们不妨将-Ze最终放在坐标的w分量上，由OpenGL替我们完成这里的除法操作，那么我们可以将这一过程写成下列形式：

　　将除以-Ze分离到w分量上操作以后，Xc和Yc就可以使用向量相乘来表示了：

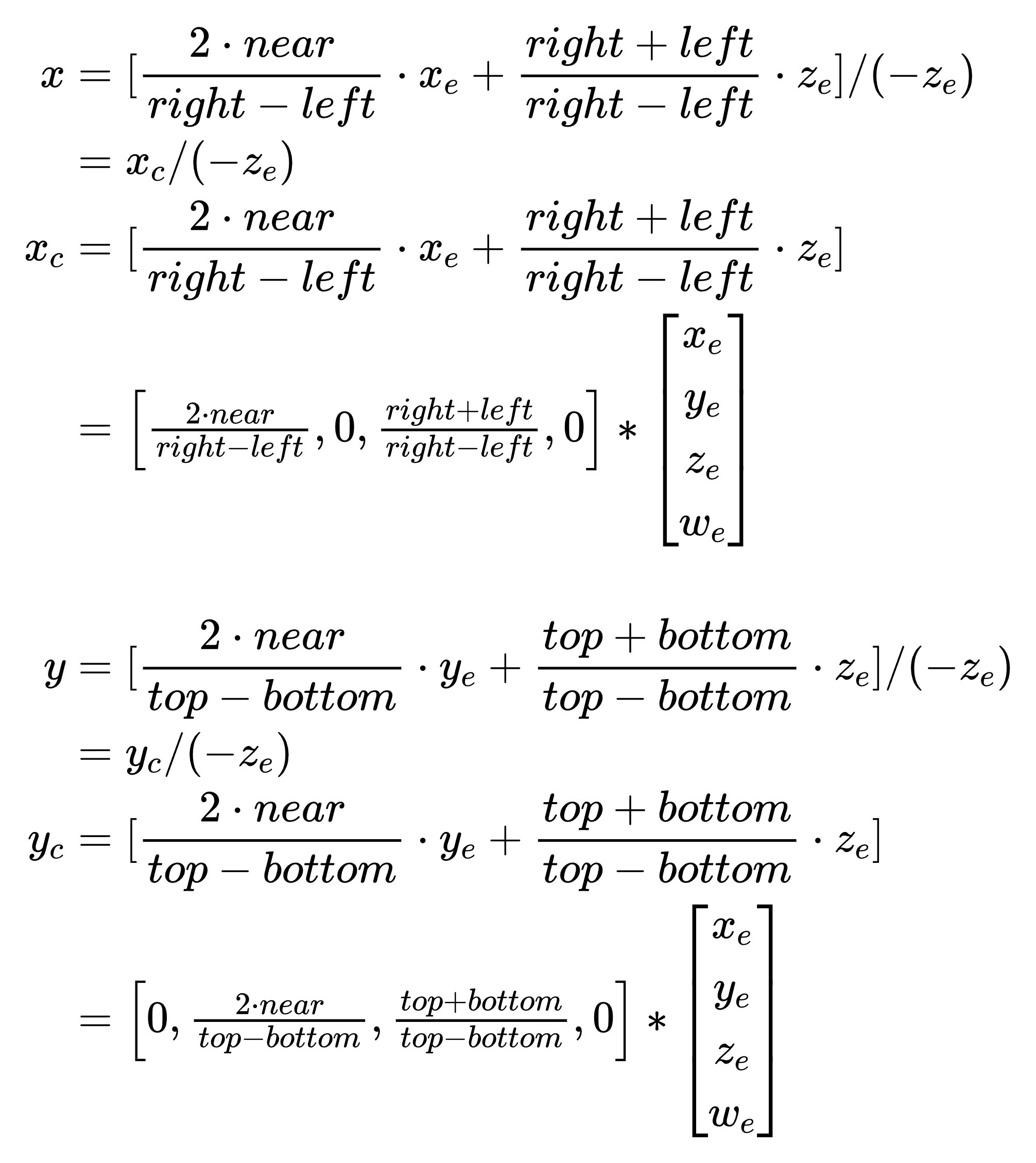
　　此时，我们已经确定了x，y，w三个分量的计算方法，我们将变换写成矩阵的形式如下：

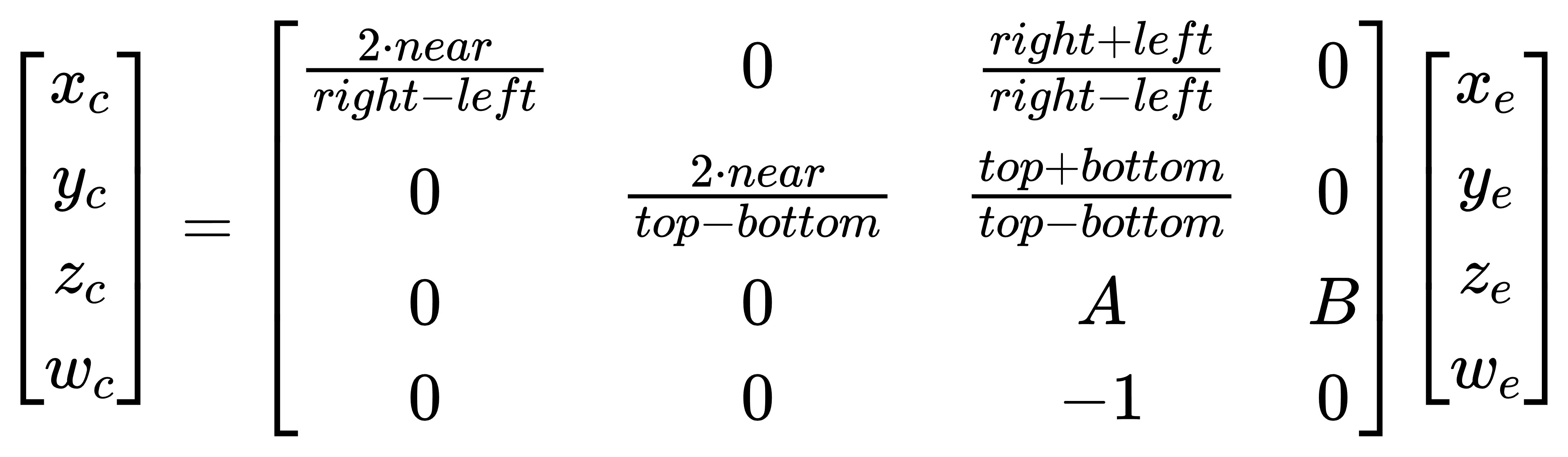
　　我们离得到最终的透视投影矩阵已经很近了，我们只需要确定z分量的计算公式即可。透视变换过程中z分量是不会改变的，也就是说通过矩阵的变换和齐次坐标系的除法，最终达到的效果只需要完成其归一化即可。我专门在上一个公式的矩阵形式写法中给z计算的位置留了两个未知数A和B。需要解释的是，z的变换只需要保证最终的结果归一化即可，显然这样的计算与x-y分量无关，这便是为什么矩阵的第三行只有两个未知数。
　　根据上述矩阵表示形式，我们可以得到完整的带有未知数的z计算公式：

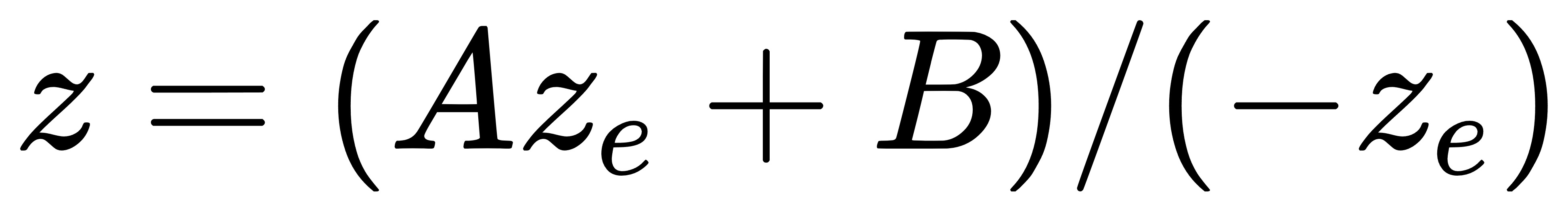
　　由边界条件可以建立方程组如下：

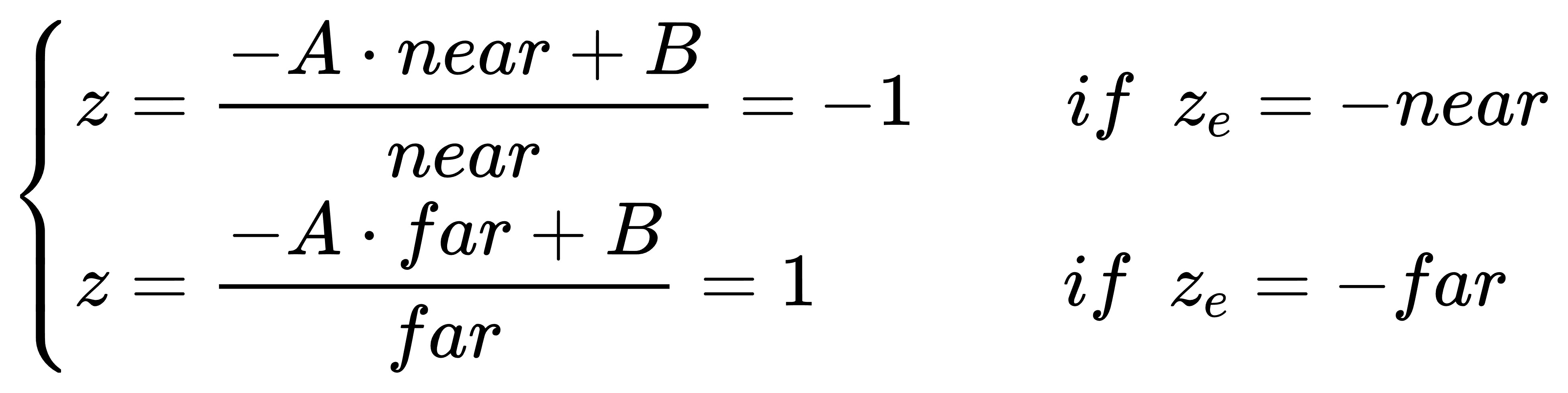
　　解方程组可得A和B的表达式：

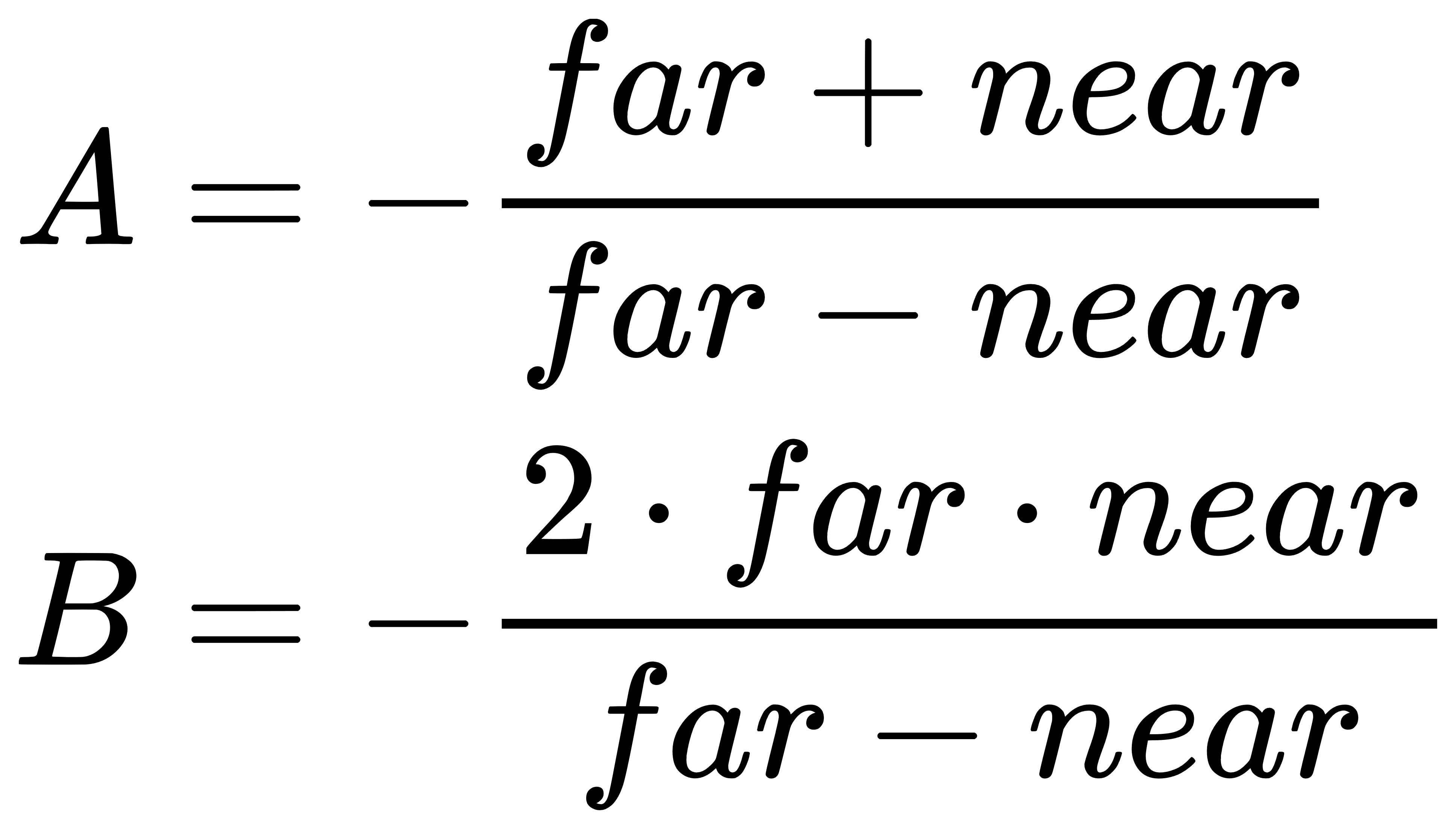
　　至此，我们得到了完整的透视投影矩阵：

　　通常情况下，视锥体的中轴线和z轴重合，上下边界对称，左右边界也对称。另外，glm库中调用生成透视投影矩阵的参数为Fov、近平面的宽高比、近平面、远平面，如下为glm库中perspective函数的声明：

template<typename T>
GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> perspective(T fovy, T aspect, T zNear, T zFar){
    // some code
}

　　即有以下通用条件：

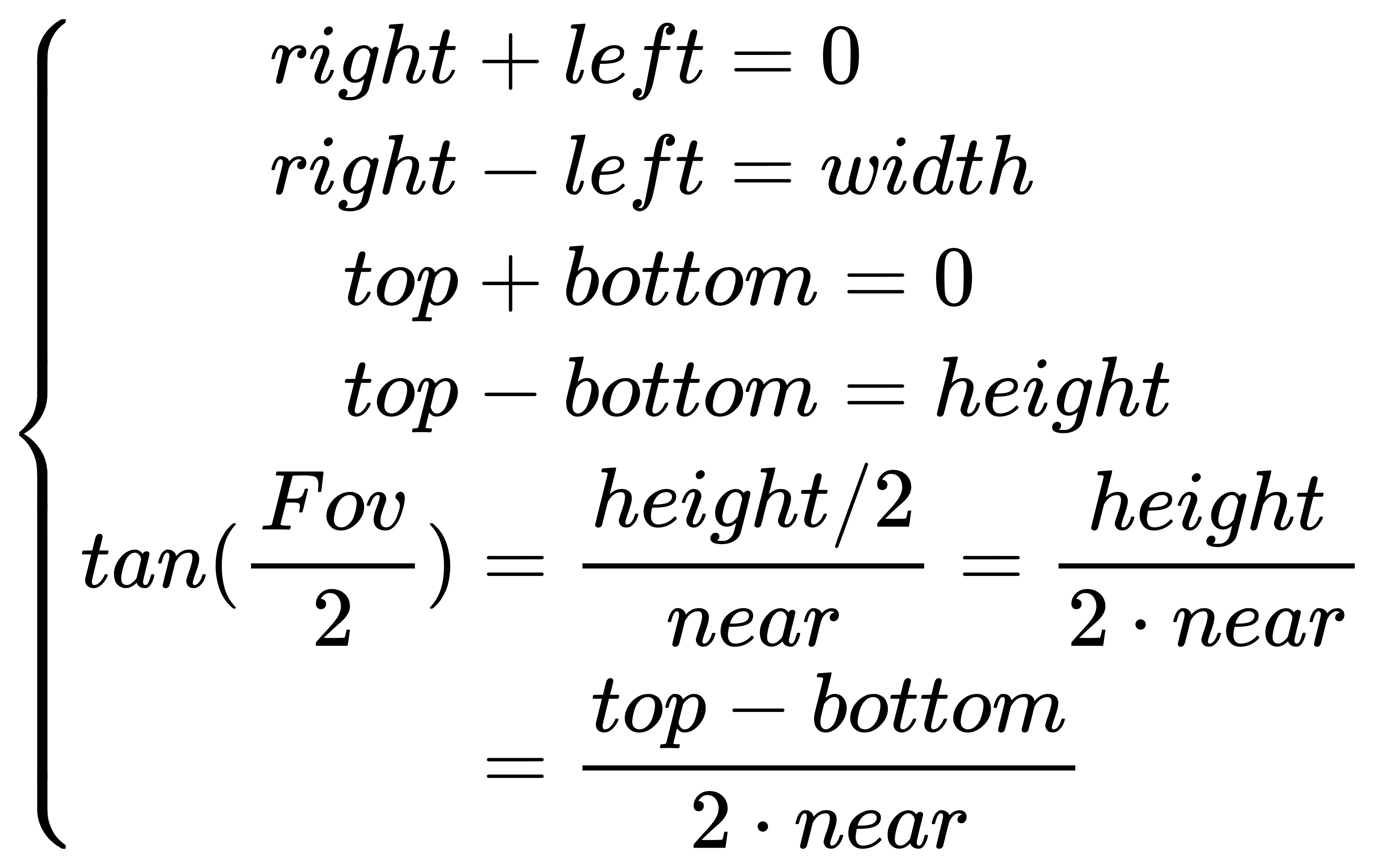
　　根据通用条件，我们可以表示矩阵的每一项如下：

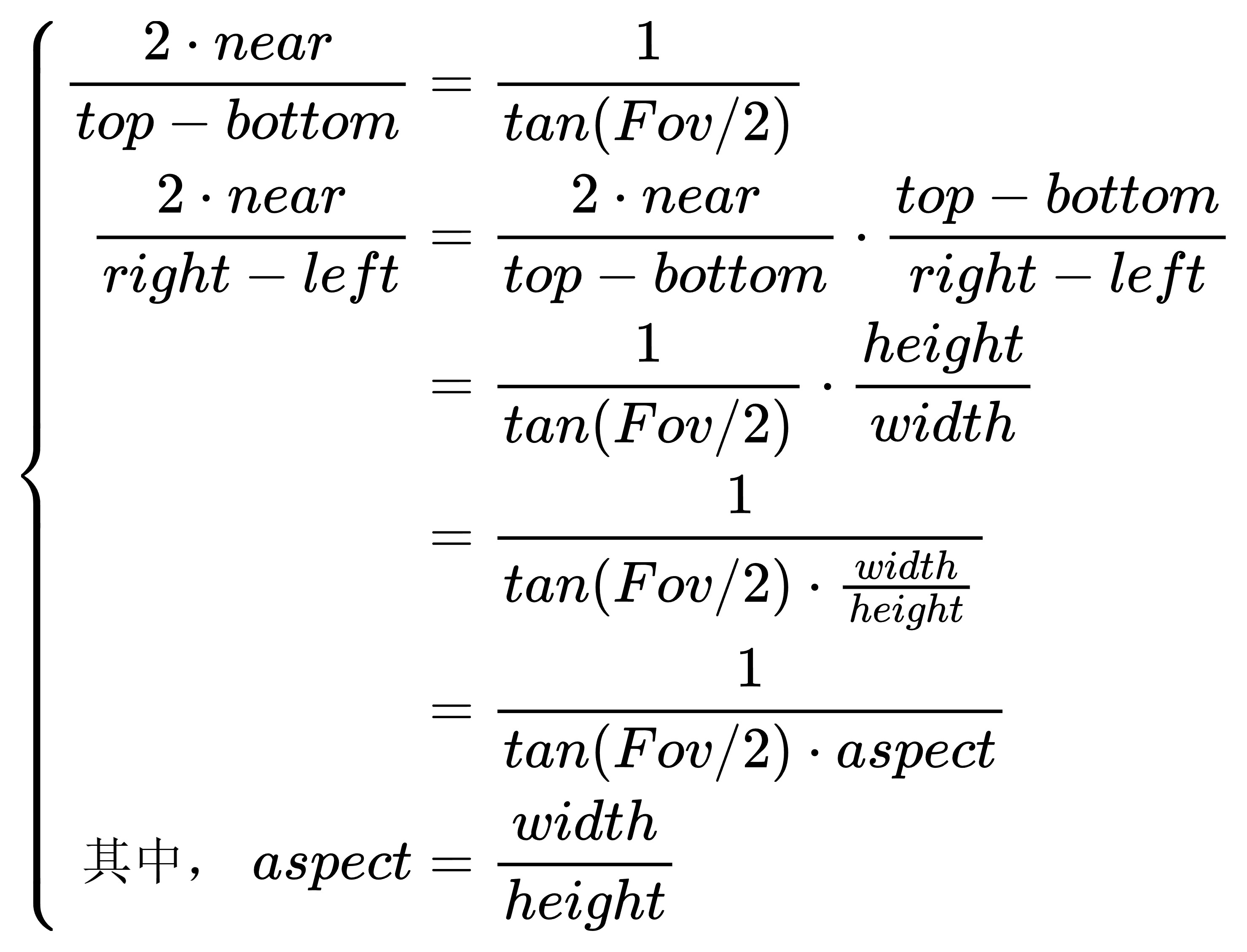
　　最终，我们得到一个使用Fov、近平面的宽高比、近平面、远平面参数表示的通用透视投影矩阵表示：

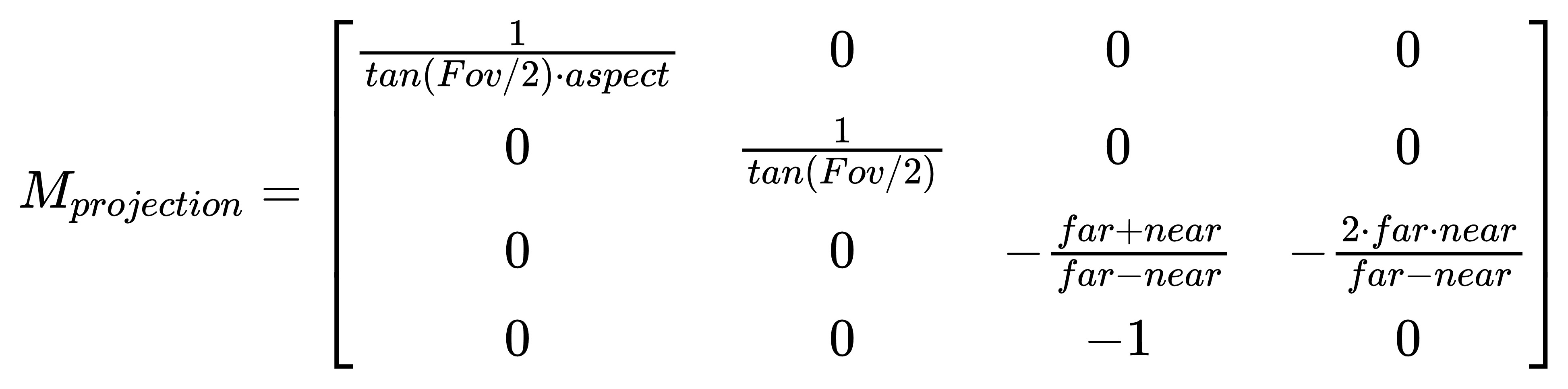
　　同样的，glm库中透视投影矩阵的实现与计算结果一致（glm库中的矩阵是列优先）：

template<typename T>
GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> perspectiveRH_NO(T fovy, T aspect, T zNear, T zFar)
{
    assert(abs(aspect - std::numeric_limits<T>::epsilon()) > static_cast<T>(0));

    T const tanHalfFovy = tan(fovy / static_cast<T>(2));

    mat<4, 4, T, defaultp> Result(static_cast<T>(0));
    Result[0][0] = static_cast<T>(1) / (aspect * tanHalfFovy);
    Result[1][1] = static_cast<T>(1) / (tanHalfFovy);
    Result[2][2] = - (zFar + zNear) / (zFar - zNear);
    Result[2][3] = - static_cast<T>(1);
    Result[3][2] = - (static_cast<T>(2) * zFar * zNear) / (zFar - zNear);
    return Result;
}

　　其实透视投影矩阵的计算，只是在正交投影计算前增加了一步对x和y坐标的透视变换，为了统一两个阶段的变换过程，计算矩阵自然变得麻烦了一些，望读者能够看懂原理之后自行推导一遍，以深化理解。