线性表
以c为主要的语言描述,但是引入了c++中“传引用”的写法,以及其他相对便捷的操作
我已对所有的函数接口进行了调试,保证可正常调用运行,但可能个别没有考虑到特殊的边界所产生的bug希望各位指正
线性表的ADT
线性表是最常见且最简单的一种数据结构。一个线性表的n个元素的有限序列。以下是线性表的ADT描述,再之后的代码实现中,仅对部分函数接口给予实现(可能会适当的对函数功能进行修改)。
//线性表的ADT描述
ADT List{
数据对象:D={ai|ai ∈ Elemset , i=1,2,3...n,n>=0}
数据关系:R1={<ai-1,ai>|ai-1,ai∈D,i=2,3...n}
基本操作:
InitList(&L)
操作结果:构造一个空的线性表。
DestroyList(&L)
初始条件:线性表L已存在。
操作结果:销毁线性表L。
ClearList(&L)
初始条件:线性表L已存在。
操作结果:将L重置为空表。
ListEmpty(L)
初始条件:线性表L已存在。
操作结果:若L为空表,返回True,否则返回false。
ListLength(L)
初始条件:线性表L已存在。
操作结果:返回L中数据元素的个数。
GetElem(L,i,&e)
初始条件:线性表L已存在,0<=i<ListLength(L)。
操作结果:用e返回L中下标为i数据元素的值。
LocateElem(L,e,compare())
初始条件:线性表L已存在,compare()是数据元素判定的比较函数。
操作结果:返回L中第一个与e满足compare的数据元素的为序。若不存在,则返回-1。
ListInsert(&L,i,e)
初始条件:线性表L已存在,1<=i<=ListLength(L)+1。
操作结果:在L中的第i个位置之前插入新的数据元素e,L的长度加1。
ListDelete(&L,i,&e)
初始条件:线性表L已存在,1<=i<=ListLength(L)。
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1。
ListTraverse(L,visit())
初始条件:线性表L已存在。
操作结果:依次对L的每个数据元素调用visit()。如果visit失败,则操作失败。
}顺序表
顺序表使用一块连续的空间存放若干数量的元素,可以随机存取,但增、删等修改性能较差。
顺序表的定义
//顺序表的定义
#define LIST_INIT_SIZE 100 //顺序表的初始化大小
typedef int Elem; //数据元素封装
typedef struct list{ //定义顺序表结构体
Elem *p; //数组空间的地址
unsigned int len; //顺序表的有效长度
}SqList;顺序表函数接口的实现
//函数接口的实现
#include<stdio.h>
#include<stdlib.h>
//顺序表的初始化
void InitList(SqList &L){ //申请一定大小的数组空间,并把地址给p
L.p=(Elem*)malloc(sizeof(Elem)*LIST_INIT_SIZE);
L.len=0; //初始化大小为0
if(L.p==NULL){ //如果分配失败,输出失败提示
printf("List init failed. Error: Memory allocation failed.\n");
exit(EXIT_FAILURE);
}
}
//销毁顺序表
void DestroyList(SqList &L){ //销毁顺序表L分配的数组空间
free(L.p);
}
//清空顺序表
void ClearList(SqList &L){ //惰性清除,即使所有的数据无效
L.len=0;
}
//顺序表判空
bool ListEmpty(SqList L){ //判断顺序表是否为空
return !L.len; //如果长度时0,为空返回!0(真),否则返回假
}
//返回顺序表的长度
unsigned int ListLength(SqList L){ //返回顺序表的长度
return L.len;
}
//返回L中第i个元素给变量e,如果成功则返回true,否则返回false
bool GetElem(const SqList L,unsigned int i,Elem &e){
if(i>=L.len) return false;
e=L.p[i];
return true;
}
//在顺序表的下标i处插入新的数据元素,插入成功返回true,否则返回false
bool ListInsert(SqList &L,unsigned int i,Elem e){
//如果插入在顺序表长度范围以外,或者顺序表已满
if(i>L.len||L.len==LIST_INIT_SIZE) return false;
for(int j=L.len;j>i;j--) //i之后的元素后移
L.p[j]=L.p[j-1];
L.p[i]=e; L.len++; //将e插入到下标i处,长度加一
return true;
}
//删除顺序表中下标为i的元素并用e返回,删除成功返回true,否则返回false
bool ListDelete(SqList &L,unsigned int i,Elem &e){
if(i>=L.len||L.len==0) return false;//如果i超出范围或者顺序表为空
e=L.p[i]; //保存删除的元素
for(int j=i;j<L.len;j++) //i号之后的元素前移
L.p[j]=L.p[j+1];
L.len--; //表长减小
return true;
}
//顺序表的遍历
void ListTraverse(SqList L){ //遍历并打印顺序表内容,访问方式可修改
for(int i=0;i<L.len;i++){
if(i) putchar(' '); //元素之间用空格隔开
printf("%d",L.p[i]);
}
}常见顺序表的算法实现
将两个递增的顺序表合并
//将两个有序(递增)的顺序表合并且返回一个新的有序的顺序表
//时间复杂度O(len_a+len_b),空间复杂度O(len_a+len_b)
SqList MergeList(SqList a,SqList b){
SqList ret; //定义一个返回值,一个顺序表
int len_a=a.len,len_b=b.len;
int i=0,j=0,index=0;
ret.len=len_a+len_b; //计算合并后的顺序表的大小
ret.p=(Elem*)malloc(sizeof(Elem)*ret.len); //申请空间
if(ret.p==NULL) exit(EXIT_FAILURE); //如果内存申请失败,返回
while(i<len_a&&j<len_b){ //比较a,b的中元素,较小的合并到ret中
if(a.p[i]<b.p[j]) ret.p[index++]=a.p[i++];
else ret.p[index++]=b.p[j++];
}
//如果有其中一个顺序表有剩余,继续合并进ret中
while(i<len_a) ret.p[index++]=a.p[i++];
while(j<len_b) ret.p[index++]=b.p[j++];
return ret;
}删除顺序表中所有值为x的元素
//删除顺序表中所有值为x的元素,并返回删除的个数
//采用惰性删除,时间复杂度O(n),空间复杂度O(1)
int Delete_x(SqList &L,Elem x){
int cnt=0,ret; //cnt为新的计数下标
for(int i=0;i<L.len;i++){ //遍历整个链表
if(L.p[i]!=x) //覆盖式删除
L.p[cnt++]=L.p[i];
}
ret=L.len-cnt; //cnt为保留的不等于x的元素个数
L.len=cnt; //更新顺序表的长度
return ret; //返回删除的x个数
}删除顺序表中值属于[s,t]的元素
//删除顺序表中值位于[s,t]之间的元素,采取惰性覆盖删除的方法
void Delete_st(SqList &L,Elem s,Elem t){
int index=0; //存储的下标
for(int i=0;i<L.len;i++){ //遍历整个顺序表
if(L.p[i]<s||L.p[i]>t) //如果不处于删除的范围内
L.p[index++]=L.p[i]; //则在数组中进行保留
}
L.len=index; //更新表的长度
}统计顺序表中的主元(出现次数超过一半的称为主元)
//统计顺序表中的主元
//在此假定前提条件顺序表不为空
Elem Majority(SqList L){
int cnt=1; //用于计数
Elem ret=L.p[0]; //ret为候选主元
for(int i=1;i<L.len;i++){ //遍历整个顺序表
if(L.p[i]==ret) cnt++; //如果等于主元,计数
else{
if(cnt>0) cnt--; //如果出现了不是主元的元素,则削弱主元的权值(计数)
else{
ret=L.p[i];cnt=1; //如果备选主元被削弱到0,则更换主元,重新计数
}
}
}
return ret;
}将线性表L在[i,j]区间内的元素逆置
//将顺序表中从下标[i,j]区间内的元素逆序
void Reverse(SqList &L,int i,int j){
while(i<j){ //i,j为两侧指针
Elem temp=L.p[i]; //交换i,j
L.p[i]=L.p[j];
L.p[j]=temp;
i++;j--; //指针向中间缩进
}
} 将线性表循环左移k个元素(借助逆置函数)
//将顺序表中的元素循环左移k个元素
void Rotate_left(SqList &L,int k){
Reverse(L,0,k-1); //先将0~k-1逆置
Reverse(L,k,L.len-1); //再将k~len-1逆置
Reverse(L,0,L.len-1); //在将整个顺序表逆置
} 测试顺序表的main函数
int main(void){
//初始化
SqList L1,L2; //定义两个顺序表L1 L2
InitList(L1);InitList(L2); //初始化两个顺序表,为其分配空间
printf("已经初始化L1和L2...\n");
//判空函数测试
printf("L1是否为空:");
if(ListEmpty(L1)) printf("为空\n");
else printf("非空\n");
Elem temp;
for(int i=20;i>=0;i--){ //为顺序表中的元素赋值
temp=i;
ListInsert(L1,0,temp); //用插入的方式为L1赋值0~20
}
for(int i=25;i>=5;i--){ //用插入的方式为L2负值5~25
temp=i;
ListInsert(L2,0,temp);
}
//顺序表 遍历测试
printf("顺序表L1内容如下:\n");
ListTraverse(L1); putchar('\n');
printf("顺序表L2内容如下:\n");
ListTraverse(L2); putchar('\n');
//顺序表合并测试
SqList L3= MergeList(L1,L2); //合并连个顺序表,并用L3存储
printf("顺序表合并如下:\n");
ListTraverse(L3); putchar('\n');
//顺序表查询和删除测试
if(GetElem(L3,5,temp)){
printf("查找下标为5的元素成功,值为:%d\n",temp);
printf("顺序表L3内容如下:\n");
ListTraverse(L3); putchar('\n');
}
printf("删除下标为10的元素:\n");
if(ListDelete(L3,10,temp)){
printf("删除下标为10的元素成功,值为:%d\n",temp);
printf("顺序表L3删除下标为10的元素后内容如下:\n");
ListTraverse(L3); putchar('\n');
}
printf("删除值属于[11,15]的元素:\n") ;
Delete_st(L3,11,15);
printf("顺序表L3删除11-15之间的元素后内容如下:\n");
ListTraverse(L3); putchar('\n');
//循环左移测试
printf("对L3循环左移6个元素测试:\n");
Rotate_left(L3,6);
printf("顺序表L3循环左移6个元素后内容如下:\n");
ListTraverse(L3); putchar('\n');
return 0;
}输出结果如下:
已经初始化L1和L2...
L1是否为空:为空
顺序表L1内容如下:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
顺序表L2内容如下:
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
顺序表合并如下:
0 1 2 3 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 17 17 18 18 19 19 20 20 21 22 23 24 25
查找下标为5的元素成功,值为:5
顺序表L3内容如下:
0 1 2 3 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 17 17 18 18 19 19 20 20 21 22 23 24 25
删除下标为10的元素:
删除下标为10的元素成功,值为:7
顺序表L3删除下标为10的元素后内容如下:
0 1 2 3 4 5 5 6 6 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 17 17 18 18 19 19 20 20 21 22 23 24 25
删除值属于[11,15]的元素:
顺序表L3删除11-15之间的元素后内容如下:
0 1 2 3 4 5 5 6 6 7 8 8 9 9 10 10 16 16 17 17 18 18 19 19 20 20 21 22 23 24 25
对L3循环左移6个元素测试:
顺序表L3循环左移6个元素后内容如下:
5 6 6 7 8 8 9 9 10 10 16 16 17 17 18 18 19 19 20 20 21 22 23 24 25 0 1 2 3 4 5链表
单链表
单链表的定义
链表使用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是练习的,也可以是不连续的)。数据元素以结点的形式存在,一个结点包含两个域:存储数据元素信息的域称为数据域;存储直接后继存储位置的域成为指针域;结点之间通过指针域连接形成单链表。
typedef int Elem; //数据封装
typedef struct information{ //结点的额外信息,这里额外信息用一个结构体描述,暂定为一个int型数值
int tag;
}Inform;
typedef struct Node{ //定义链表结点
Elem data; //数据域
struct Node *next; //指针域
Inform info; //结点的额外信息
}LNode,*LinkList;
//定义Elem类型的打印输出函数
void PrintData(Elem e){
printf("%d",e);
}单链表函数接口的实现
不带头结点的写法:
不带头结点的情况下,链表指针指向第一个结点(空时为NULL),此使链表可能因为增删等原因导致链表指针发生改变。
//初始化链表
void InitList(LinkList &L){
L=NULL; //将链表置空
}
//销毁整个链表,并释放整个链表的内存空间
void DestoryList(LinkList &L){
while(L){
LNode *temp=L; //使用temp接管链表
L=L->next; //工作指针后移
free(temp); //释放节点
}
}
//判断链表是否为空
bool IsEmpty(LinkList L){
return !L; //如果链表指针为NULL则为空,否则不是空
}
//链表判满
bool IsFull(LinkList L){ //这里判定内存池中是否还有空间容纳节点来判断是否满
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return true; //如果申请内存失败,则为满
else{ //否则,释放尝试申请的内存空间,并返回不满
free(temp);
return false;
}
}
//返回链表长度
int ListLength(LinkList L){
LNode *p=L; //p为工作指针
int cnt=0; //cnt为节点计数器
while(p){ //当p不空时,工作指针步进并计数
p=p->next;
cnt++;
}
return cnt;
}
//读取链表的第i个元素(i从1开始),并用参数e接收,如果读取失败返回false,否则返回true
bool GetElem(LinkList L,int i,Elem &e){
if(i<=0||i>ListLength(L)){ //如果读取的位置不合法,打印越界错误
printf("Error: index out of range.\n");
return false;
}
LNode *p=L;
while(--i) //循环i次获取该位置的元素
p=p->next;
e=p->data;
return true; //读取成功
}
//返回第一个数据等于x的节点的序号(从1开始),如果不存在则返回-1
int LocateElem(LinkList L,Elem x){
int index=0;
while(L){ //指针步进,index用于计数
index++;
if(L->data==x) return index; //如果找到第一个等于x的则返回序号
L=L->next;
}
return -1; //找不到 返回-1;
}
//在链表中插入一个元素x,(头插),操作成功返回true,否则返回false
bool HeadInsert(LinkList &L,Elem x){
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return false; //如果内存申请失败,则返回false,无法插入
temp->data=x; //头插代码
temp->next=L;
L=temp;
return true; //插入成功
}
//在链表中插入一个元素x,(尾插),操作成功返回true,否则返回false
bool TailInsert(LinkList &L,Elem x){
LNode *tail=L; //tail是记录最后一个节点的指针
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return false; //如果内存申请失败,则返回false,无法插入
temp->data=x;temp->next=NULL;
if(tail==NULL){ //如果链表为空,则让L等于新节点
L=temp;
}
else{ //如果不为空
while(tail->next) //找到最后一个节点
tail=tail->next;
tail->next=temp; //插入节点
}
return true;
}
//在链表中第i个位置插入一个元素x(从1开始),如果成功返回true,否则返回false
bool InsertList_i(LinkList &L,unsigned int i,Elem x){
int len=ListLength(L);
LNode *temp=(LNode*)malloc(sizeof(LNode));//为插入的元素申请结点空间
LNode *p=L;
if(len==0||i>len+1||i<=0||temp==NULL)
return false; //如果链表为空或者满,或者i越界则插入失败,如果链表场Len,可以在尾部即Len+1位置上插入
temp->data=x; //结点赋值
if(i==1){ //没有头结点,所以插入第一个做特殊处理
temp->next=L;
L=temp;
}
else{
i--; //找到第i-1个结点
while(--i)
p=p->next;
temp->next=p->next; //新节点接管i之后的链表
p->next=temp; //将新节点勾链到i-1上
}
return true;
}
//删除链表中第一个i个(从1开始)的数据元素,并用e返回其值,成功则返回true,否则返回false
bool DeleteList_i(LinkList &L,unsigned int i,Elem &e){
int len=ListLength(L);
if(len==0||i>len||i<=0) //如果链表为空,或者i越界则删除失败
return false;
LNode* p=L; //工作指针
if(i==1){ //没有头结点,所以删除第一个需要特殊处理
e=L->data;
L=L->next;
free(p);
}
else{
i--;
while(--i) //找到第i-1个结点
p=p->next;
LNode *temp=p->next; //temp指向第i个结点
e=temp->data;
p->next=temp->next; //第i-1和第i+1个结点勾链
free(temp); //释放删除的结点
}
return true;
}
//遍历整个链表,并打印链表的结构,具体打印的访问细节,可自行实现
void TraverseList(LinkList L){
int cnt=0;
while(L){
if(cnt++) printf("->");
PrintData(L->data);
L=L->next;
}
}带头结点的写法:
带头结点的情况下,链表指针指向一个空的结点,该空结点数据域不保存数据元素,指针域指向链表的第一个结点(初始为NULL)。通常来说带头结点的链表各种操作实现容易,且易于理解,因此之后的常见算法按照带头结点的链表给予实现。
//初始化链表,若初始化成功返回true,否则返回false
bool InitList(LinkList &L){ //为链表申请并初始化一个头结点,然后初始化头结点指针与为null
L=(LNode*)malloc(sizeof(LNode));//申请头结点空间
if(L==NULL) return false; //如果申请失败
L->next=NULL; //成功则,初始化指针域
return true;
}
//销毁整个链表,并释放整个链表的内存空间
void DestoryList(LinkList &L){
while(L){
LNode *temp=L; //使用temp接管链表
L=L->next; //工作指针后移
free(temp); //释放节点
}
}
//判断链表是否为空
bool IsEmpty(LinkList L){
return !L->next; //如果头结点的指针域为NULL则为空,否则不是空
}
//链表判满
bool IsFull(LinkList L){ //这里判定内存池中是否还有空间容纳节点来判断是否满
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return true; //如果申请内存失败,则为满
else{ //否则,释放尝试申请的内存空间,并返回不满
free(temp);
return false;
}
}
//返回链表长度
int ListLength(LinkList L){
LNode *p=L->next; //p为工作指针
int cnt=0; //cnt为节点计数器
while(p){ //当p不空时,工作指针步进并计数
p=p->next;
cnt++;
}
return cnt;
}
//读取链表的第i个元素(i从1开始),并用参数e接收,如果读取失败返回false,否则返回true
bool GetElem(LinkList L,int i,Elem &e){
if(i<=0||i>ListLength(L)){ //如果读取的位置不合法,打印越界错误
printf("Error: index out of range.\n");
return false;
}
LNode *p=L->next;
while(--i) //循环i次获取该位置的元素
p=p->next;
e=p->data;
return true; //读取成功
}
//返回第一个数据等于x的节点的序号(从1开始),如果不存在则返回-1
int LocateElem(LinkList L,Elem x){
int index=0;
L=L->next;
while(L){ //指针步进,index用于计数
index++;
if(L->data==x) return index; //如果找到第一个等于x的则返回序号
L=L->next;
}
return -1; //找不到 返回-1;
}
//在链表中插入一个元素x,(头插),操作成功返回true,否则返回false
bool HeadInsert(LinkList &L,Elem x){
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return false; //如果内存申请失败,则返回false,无法插入
temp->data=x; //头插代码
temp->next=L->next;
L->next=temp;
return true; //插入成功
}
//在链表中插入一个元素x,(尾插),操作成功返回true,否则返回false
bool TailInsert(LinkList &L,Elem x){
LNode *tail=L->next; //tail是记录最后一个节点的指针
LNode *temp=(LNode *)malloc(sizeof(LNode));
if(temp==NULL) return false; //如果内存申请失败,则返回false,无法插入
temp->data=x;temp->next=NULL; //因为插入到尾部,所以直接初始化指针域为NULL
if(tail==NULL){ //如果链表为空,则让第一个结点为新插入的节点
L->next=temp;
}
else{ //如果不为空
while(tail->next) //找到最后一个节点
tail=tail->next;
tail->next=temp; //插入节点
}
return true;
}
//在链表中第i个位置插入一个元素x(从1开始),如果成功返回true,否则返回false
bool InsertList_i(LinkList L,unsigned int i,Elem x){
int len=ListLength(L);
LNode *temp=(LNode*)malloc(sizeof(LNode));//为插入的元素申请结点空间
LNode *p=L; //工作指针
if(i>len+1||i<=0||temp==NULL)
return false; //如果链表为满,或者i越界则插入失败,如果链表长Len,可以在尾部即Len+1位置上插入
temp->data=x; //结点赋值
while(--i) //找到第i-1个结点
p=p->next;
temp->next=p->next; //新节点接管i之后的链表
p->next=temp; //将新节点勾链到i-1上
return true;
}
//删除链表中第一个i个(从1开始)的数据元素,并用e返回其值,成功则返回true,否则返回false
bool DeleteList_i(LinkList L,unsigned int i,Elem &e){
int len=ListLength(L);
if(len==0||i>len||i<=0) //如果链表为空,或者i越界则删除失败
return false;
LNode* p=L; //工作指针
while(--i) //找到第i-1个结点
p=p->next;
LNode *temp=p->next; //temp指向第i个结点
e=temp->data;
p->next=temp->next; //第i-1和第i+1个结点勾链
free(temp); //释放删除的结点
return true;
}
//遍历整个链表,并打印链表的结构,具体打印的访问细节,可根据定义自行实现
void TraverseList(LinkList L){
int cnt=0;
L=L->next;
while(L){
if(cnt++) printf("->");
PrintData(L->data);
L=L->next;
}
}常见链表算法的实现
//带头节点的单链表L,删除所有的元素 x并释放其空间,其中x不止一个
void Delete_x(LinkList &L,Elem x){
LNode *pre=L,*p=L->next,*temp; //pre是前一个节点的指针,p是工作指针,temp是临时指针,用于指向要删除的节点空间
while(p!=NULL){ //当p非空是遍历链表
if(p->data==x){ //如果当前节点是删除的节点
temp=p; //保存当前节点的地址
p=p->next; //删除操作
pre->next=p;
free(temp); //释放空间
}
else{
pre=p; p=p->next; //否者pre和p步进到下一个姐点
}
}
}
//带头节点的单链表L,删除所有的元素 位于s~t之间的节点并释放其空间,s和t大小顺序可以随意
void Delete_st(LinkList &L,Elem s,Elem t){
if(s>t){ //如果s比t大,则交换s和t,使得保证s小于等于t
Elem tmp=t; t=s; s=tmp;
}
LNode *pre=L,*p=L->next,*temp; //pre是前一个节点的指针,p是工作指针,temp是临时指针,用于指向要删除的节点空间
while(p!=NULL){ //当p非空是遍历链表
if(p->data>=s&&p->data<=t){ //如果当前节点是删除的节点
temp=p; //保存当前节点的地址
p=p->next; //删除操作
pre->next=p;
free(temp); //释放空间
}
else{
pre=p; p=p->next; //否则pre和p步进到下一个姐点
}
}
}
//带头结点的单链表L,逆序遍历输出L(使用递归实现)
void R_TraverseList(LinkList L){
static int count=0; //用于计数,保证输出的间隔
L=L->next; //由于带有头结点,所以要提前步进
if(L->next!=NULL) //递归边界
R_TraverseList(L);
if(count++) printf("->");
PrintData(L->data); //输出节点信息
}
//带头结点的单链表L,实现就地逆置(即空间复杂度为O(1))
void Reverse(LinkList L){
LNode *p,*r; //p为工作指针,r存放p的后继,保证不断链
p=L->next; //p从链表的第一个节点开始
L->next=NULL; //取下头结点
while(p!=NULL){ //遍历链表
r=p->next; //保存p的后继
p->next=L->next; //头插代码
L->next=p;
p=r; //p后移
}
}
//带头结点的单链表L,每k个元素逆置,不足k个的不用逆置
void K_Reverse(LinkList L,const unsigned int k){
int cnt=0,len=ListLength(L); //cnt用于计数,len表示链表长度
if(len==0||k==0||len<k) return; //如果为空链表,或者k是0,或者链表长度小于k,则不需要处理
LNode *p=L->next; //p为工作指针,初始化为第一个结点
LNode *head=L; //head为每一个k长度链表的表头结点
LNode *rear=L->next; //rear为每一个k长度链表的尾结点
L->next=NULL; //把头结点摘掉
int dealnum=len-len%k; //需要处理的k的整数倍个结点个数
while(cnt!=dealnum){ //cnt用于保证只逆置整k个结点,剩余不足k个的不做逆置处理
LNode *temp=p->next; //temp用于保证不掉链
p->next=head->next; //当前k长度的结点 使用头插的方法进行逆置处理
head->next=p;
p=temp; //p步进
cnt++; //处理节点计数
if(cnt%k==0){ //如果已经处理了k个,则更新head和rear
head=rear; //逆置后上一段k个结点的第一个成了最后一个
rear=temp; //本段的最后一个结点时该段的第一个结点
}
}
if(cnt!=len) //如果还有剩余不足k个的,直接勾链不做处理
head->next=rear;
}
//带头结点的单链表L,输出倒数第k(从1开始)个位置的结点,如果找到则输出,否则输出Not Found
void R_Search(LinkList L,const unsigned int k){
if(k==0){ //如果k是0则找不到
printf("Not Found"); return;
}
LNode *p=L->next,*q=L->next; //p和q两个工作指针,使得p比q提前步进k次,这样p到达null时,q刚好在倒数第k个
int count=0; //count用于计数
while(p!=NULL){
if(count<k) count++; //如果p步进还没达到k次,则只步进p
else q=q->next; //如果p已经提前步进k次,则p和q同时步进
p=p->next; //p不论如何倒要步进
}
if(count<k) printf("Not Found\n"); //如果count再k步之内走到结尾,说明k超过了链表长度,找不到
else PrintData(q->data); //如果找到则输出结点信息
}测试单链表的main函数
用于测试的main函数都调用了带头结点的函数和接口实现,因此使用时的函数声明请统一使用带头结点的写法。
需要使用
std命名空间,并且包含string头文件,以便于main函数内打印分割线。int main(void){
//分隔符
string str="--------------------------------------------------------------------------";
LinkList L;
InitList(L); //初始化单链表
cout<<str<<endl;
printf("初始化后的链表长度为 %d 。\n",ListLength(L));
Elem temp,temp1,temp2; //定义一些用到的结点数据元素
for(int i=0;i<20;i++){ //构造一个链表,数据为0~19
temp=i;
if(i<10) HeadInsert(L,temp); //前10个元素使用头插
else TailInsert(L,temp); //后十个元素使用尾插
}
//输出链表构建好的链表结构,调用链表长度函数和链表遍历函数
printf("链表长度为 %d ,其结构如下:\n",ListLength(L));
TraverseList(L);
cout<<str<<endl;
printf("读取链表的第10个元素(从1开始计算),并用temp接收:");
GetElem(L,10,temp);
PrintData(temp); putchar('\n'); //输出temp结点数据并换行
cout<<str<<endl;
temp=13;
printf("链表中结点数据等于temp(其中值为13)的序号为: %d\n",LocateElem(L,temp));
temp=99;
printf("链表中没有结点数据等于temp(其中值为99)的,因此打印: %d\n",LocateElem(L,temp));
cout<<str<<endl;
temp=66;
printf("在链表中第3个位置插入一个结点数值为66的结点,插入后链表结构为:\n");
InsertList_i(L,3,temp);
TraverseList(L);
cout<<str<<endl;
printf("删除链表中第4个结点(从1开始计算),并用temp返回其值:");
DeleteList_i(L,4,temp);
PrintData(temp); putchar('\n'); //输出删除的结点信息并换行
printf("删除后的链表结构如下:\n");
TraverseList(L);
cout<<str<<endl;
temp1=10,temp2=14;
Delete_st(L,temp1,temp2);
printf("删除链表中值位于10~14的结点,删除后的链表结构如下:\n");
TraverseList(L);
cout<<str<<endl;
printf("逆序输出链表,结果如下:\n");
R_TraverseList(L); putchar('\n');
cout<<str<<endl;
printf("链表整体逆置,逆置之后的链表结构如下:\n");
TraverseList(L);
cout<<str<<endl;
printf("链表每K个逆置,结尾处不足k个的不用逆置,每4个逆置结果如下:\n");
K_Reverse(L,4);
TraverseList(L);
cout<<str<<endl;
printf("输出倒数第k个结点元素,这里k取值为4,结果如下:");
R_Search(L,4); putchar('\n');
cout<<str<<endl;
return 0;
}输出结果如下:
--------------------------------------------------------------------------
初始化后的链表长度为 0 。
链表长度为 20 ,其结构如下:
9->8->7->6->5->4->3->2->1->0->10->11->12->13->14->15->16->17->18->19
--------------------------------------------------------------------------
读取链表的第10个元素(从1开始计算),并用temp接收:0
--------------------------------------------------------------------------
链表中结点数据等于temp(其中值为13)的序号为: 14
链表中没有结点数据等于temp(其中值为99)的,因此打印: -1
--------------------------------------------------------------------------
在链表中第3个位置插入一个结点数值为66的结点,插入后链表结构为:
9->8->66->7->6->5->4->3->2->1->0->10->11->12->13->14->15->16->17->18->19
--------------------------------------------------------------------------
删除链表中第4个结点(从1开始计算),并用temp返回其值:7
删除后的链表结构如下:
9->8->66->6->5->4->3->2->1->0->10->11->12->13->14->15->16->17->18->19
--------------------------------------------------------------------------
删除链表中值位于10~14的结点,删除后的链表结构如下:
9->8->66->6->5->4->3->2->1->0->15->16->17->18->19
--------------------------------------------------------------------------
逆序输出链表,结果如下:
19->18->17->16->15->0->1->2->3->4->5->6->66->8->9
--------------------------------------------------------------------------
链表整体逆置,逆置之后的链表结构如下:
9->8->66->6->5->4->3->2->1->0->15->16->17->18->19
--------------------------------------------------------------------------
链表每K个逆置,结尾处不足k个的不用逆置,每4个逆置结果如下:
6->66->8->9->2->3->4->5->16->15->0->1->17->18->19
--------------------------------------------------------------------------
输出倒数第k个结点元素,这里k取值为4,结果如下:1
--------------------------------------------------------------------------单链表算法补充(伪代码)
1.拆分问题
设带头结点的单链表A={a1,b1,a2,b2,a3,b3...an,bn},将其拆分为带头结点的链表A={a1,a2,a3,a4,a5...an}和B={bn,bn-1,bn-2...b1},其中B作为返回值返回带头结点的单链表头指针。
//算法思想:
//将链表A的头结点摘下,然后建立B的头结点,由于链表元素个数为偶数
//所以将奇数号元素尾插到A中,将偶数号元素头插到B链表中,最后返回链表B
LinkList Dis_creat(LinkList A){
LinkList B=(LinkList)malloc(sizeof(LNode)); //申请链表B的头结点空间
B->next=NULL; //B链表初始化头结点的指针域为NULL
LinkList p=A->next; //p为工作遍历指针,从A的第一个元素开始
LinkList q,ra=A; //q为保证不断链的指针,ra为链表A执行尾插的时候的尾指针,初始化为A
while(p!=NULL){ //每次处理两个元素,这样第一个先处理a,第二个处理B
ra->next=p;ra=p; //A尾插代码
p=p->next; //工作指针p步进
q=p->next; //防止断链
p->next=B->next; //对链表B进行头插,使得最终顺序为从n到1的逆序
B->next=p;
p=q; //更新p指针
}
ra->next=NULL; //把链表A的最后一个指针域置空
return B; //返回B
} 2.求两个链表的并
两个递增链表,合并为一个递减单链表,要求使用原来的链表节点存放数据元素。
//算法思想:
//先将第一个链表的头结点摘下,接下俩将所有的节点存放到第一个链表中。
//两个工作指针依次推进两个链表,将两个链表合并到第一个链表中。
//由于两个链表递增,所以比较选择较小的那个头插入第一个链表中。
void MergeList(LinkList La,LinkList Lb){
LinkList q,pa=La->next;pb=Lb->next; //使用q作为勾链时防止断链的指针,pa,pb为两个链表的工作指针
La->next=NULL; //由于采用头插的方法插入到La中,所以将la的头指针摘下来,并初始为NULL
while(pa&&pb){ //当两个链表的工作指针都没有到尾部时,进行比较
if(pa->data<pb->data){ //比较元素大小,如果a中元素小,将其头插到LA中
q=pa->next; //防止断链
pa->next=La->next; //头插代码
La->next=pa;
pa=q; //更新pa
}
else{ //同理如果Lb中的元素小,将其头插到Lb中
q=pb->next;
pb->next=La->next;
La->next=pb;
pb=q;
}
} //while循环结束后,至多有一个链表还有剩余
if(pb) pa=pb; //为了减少代码重复,如果是b还有剩余,将其交予pa指针,统一处理时候的代码
while(pa){ //将链表中剩余的元素依次头插到链表中去
q=pa->next;
pa->next=La->next;
La->next=pa;
pa=q;
}
free(Lb); //B链表不再使用,释放B的头结点空间
} 3.求两个链表的交
A、B两个带头结点的单链表,元素递增有序,A和B中产生C来存放共同元素(不能破坏A、B中的节点)。
//算法思想:
//创建新链表C用于存放共同元素
//A、B各自有工作指针后移并做比较:
//①如果比较结果不相等,由于链表有序,所以元素较小的链表工作指针后移
//②如果比较结果相等,创建新节点并复制共同的数据元素,尾插入C中,然后A、B的工作指针同时向后移动
LinkList Get_common(LinkList A,LinkList B){
LinkList C=(LinkList)malloc(sizeof(LNode)); //创建新的链表头节点
LinkList r=C,pa,pb,tmp; //r用于尾插,初始化为C,pa、pb为工作指针,tmp为存放共同元素的临时指针
while(pa&&pb){
if(pa->data!=pb->data){ //如果不相同
if(pa->data<pb->data) //如果a中元素较小,则a指针向后移动
pa=pa->next;
else //否则b指针向后移动
pb=pb->next;
}
else{ //如果相同
tmp=(LinkList)malloc(sizeof(LNode)); //创建新的节点
tmp->data=pa->data; //复制数据元素
r=>next=tmp; //尾插
r=tmp;
pa=pa->next; pb=pb->next; //a和b的指针同时向后移动
}
}
r->next=NULL; //c链表的最后一个指针域置空
return C; //返回链表C
} 4.字符序列匹配
两个使用链表存储的字符序列A和B,判定B是否为A中的子序列。(两个链表均无头指针)
//算法思想:
//由于是单链表,所以使用简单匹配的方法进行模式串的匹配
//如果某一个结点相同,继续向后匹配;如果不同,则A串返回到此次匹配起点的下一个位置,B回到第一个结点
bool Pattern(LinkList A,LinkList B){
LinkList p=A,q=B; //p和q分别为A和B的工作指针
LinkList pre=p; //pre记录每一次匹配的起始位置
while(p&&q){ //当两个链表都未到结尾的时候进行匹配
if(p->data==q->data){ //如果结点中的元素相同
p=p->next; //p和q工作指针同时后移
q=q->next;
}
else{ //一旦不匹配
pre=pre->next; //pre更新
p=pre; //更新p和q指针
q=B;
}
}
if(q==NULL) return true; //如果匹配返回真,否则返回假
else return false;
} 5.寻找两个链表的公共结点
现有两个链表,如果有相同的后缀,则公共后缀部分共享相同的链表结点。请设计一个算法找出两个链表的公共结点,如果存在则返回公共结点的指针,否则返回NULL。(两个链表无头结点)
//方法一
//算法思想:
//具有公共后缀部分的链表,共享尾部,所以需要先判断尾部可能的起始位置
//因为可能两个链表的长度不同,所以先求出两个链表的长度差,然后将两者右对齐,从对齐处开始进行比对
//求出长度,根据长度差,将长一些的先行遍历长出的一部分,然后再同步比对
int Getlength(LinkList L){ //计算链表长度
int len=0;
while(L->next!=NULL){
len++;
L=L->next;
}
return len;
}
LinkList Search_first_commen(LinkList L1,LinkList L2){
int len1=Getlength(L1),len2=Getlength(L2); //计算两个链表的长度
int dist=len2-len1; //计算长度差
if(Len1<len2){ //如果第二个链表更长一些,dist为负值,则交换L1和L2,并使dist为正
LinkList tmp=L1; //这样不论怎样都是的L1为长链表,L2为短链表,代码可以统一起来
L1=L2;
L2=tmp;
dist=-dist;
}
while(dist--) L1=L1->next; //长链表先后移长度差的距离
while(L1->next!=NULL&&L1->next!=L2->next){ //开始比较,如果没有到达结尾,或者下一个结点还不是公共结点
L1=L1->next; L2=L2->next; //则指针都向后移动
}
return L1->next; //返回公共结点,当while循环结束时,要么下一个既是公共结点,要么就是到了结尾处,即没有公共节点的情况
}
//方法二
//算法思想:
//使用空间换时间的思路,为链表节点增加一个访问标记信息info,默认已初始化为0。
//先遍历第一个链表,访问过程中把所有的节点的标记信息修改为1
//再遍历第二个链表,如果访问标记信息已经为1,则表示该节点便是公共后缀的第一个节点,返回指针即可
LinkList search_first_common(LinkList L1,LinkList L2){
int ret=NULL;
while(L1){ //先遍历第一个链表,并标记访问信息
L1->info=1;
L1=L1->next;
}
while(L2){ //再遍历第二个链表,判断访问标记是否被修改过
if(L2->info==1){ //如果再第一次访问的时候已被标记,则当前节点为第一个公共节点
ret=L2;break; //对返回只进行赋值,并结束循环
}
L2=L2->next;
}
return ret; //如果没有公共后缀,则ret的之不会被修改,即NULL
}循环链表
循环链表时另一种形式的链式存储结构。其特点是表中最后一个结点的指针域指向头结点,使整个链表形成一个环,从任意一个结点可以到达表中其他的结点。
循环链表的操作和线性链表基本一致,主要差别时在循环条件的判别上,对于循环链表来说:
//假设对于带头结点的循环链表L,工作指针为p
//判断链表为空
if(L->next==L) return true; //如果为空
else return false; //如果不空
//判断链表是否到了结尾的判断条件
p->next==L; //如果工作指针的下一个位置到了表头结点则遍历结束循环链表的算法(伪代码)
1.两个循环链表的合并
已知两个具有头结点的循环链表,链表的头结点的指针分别为h1和h2,写一个函数将h2链接到h1之后,链接后保持链表的循环形式。
//算法思想
//根据循环链表的判断条件,找到h1和h2的最后一个节点,然后将h2勾链,并形成封闭的循环
void MergeCLink(LinkList h1,LinkList h2){
LinkList p=h1,q=h2;
while(p->next!=h1) p=p->next; //找到h1和h2的最后一个节点
while(q->next!=h2) q=q->next;
p->next=h2->next; free(h2); //将h2连接到h1的尾部,释放h2的头结点
q->next=h1; //将h2的最后一个节点的指针域改为h1,形成循环形式
}双向链表
非循环双向链表
双向循环链表的的指针包含一个指向前驱的指针和一个指向后继的指针,由此可以分别向前或者向后进行遍历。
非循环双向链表的算法(伪代码)
1.用带头结点的非循环双链表建立一个频度有限的排序函数
设头指针为L的带头结点的非循环双链表,每个节点有pre(前驱指针)、data(数据域)、next(后继指针)、freq(访问频度域),其中访问频度域在链表启用前初始化为0,当Locate(L,x)函数运算一次,则令值为x的的节点中freq的值增加1,并使得链表以freq非增的顺序排序,最近访问的节点排在频度相同的结点前面,以便频繁访问的结点总靠近表头,编写Locate(L,x),返回找到的结点地址,类型为指针类型。
结点类型描述。
typedef struct DNode{
Elem data;
struct DNode *pre,*next;
int freq;
}DNode,*DLinkList;算法:
//算法思想:
//每次遍历查找x所在的结点,如果查不到值x,则输出查找失败信息
//如果查找到x值所在的结点,将该结点的freq的加一
//然后向前找到第一个freq大于当前结点的结点,然后把当前结点插入其后
DLinkList Locate(DLinkList L,Elem x){
DNode *p=L->next; //p为从前向后遍历的工作指针
DNode *q; //q为向前查询的指针
while(p&&p->data!=x) p=p->next; //遍历查询值x
if(p==NULL){
printf("Not Find!"); //如果未查到,返回NULL
}
else{
p->freq++; //值为x的访问频度加1
p->next->pre=p->next; //从链表中”删除“当前结点,即将p的前驱和后继勾链
p->pre->next=p->next;
q=p->pre; //初始化q为p的前驱,并向前寻找到第一个大于当前freq的的结点,或者找到头结点结束循环
while(q!=L&&q->freq<=p->freq) q=q->pre;
p->next=q->next; //将p插入到q的下一个位置
q->next->pre=p;
p->pre=q;
q->next=p;
}
return p; //返回p,或者为空,或者为查找到的位置
}双向循环链表的定义和实现(带头结点)
双向循环链表的的指针包含一个指向前驱的指针和一个指向后继的指针,并且头节点的前驱为尾指针,尾指针的后继为头结点。因此,只需对单链表的结点定义做适当的修改即可,Elem的定义不需要改动:
typedef struct DuNode{ //定义双向链表结点
Elem data; //数据域
struct DuNode *pre; //前驱结点指针
struct DuNode *next; //后继结点指针
Inform info; //结点的额外信息
}DULNode,*DULinkList;其中,仅仅涉及单向操作的算法实现方法与单链表类似,只有插入和删除时的勾链操作有所不同,因此这里仅仅对遍历、删除和插入结点给出实现方法:
//基本操作
//初始化链表
bool InitList_Du(DuLinkList &L){ //为链表申请并初始化一个头结点,然后初始化头结点指针与为null
L=(DuLNode*)malloc(sizeof(DuLNode)); //申请头结点空间
if(L==NULL) return false; //如果申请失败
L->next=L; //成功则初始化指针域
L->pre=L;
return true;
}
//遍历循环双向链表
void TraverseList_Du(DuLinkList L){
int cnt=0;
DuLNode *p=L->next;
printf("head:");
while(p!=L){
if(cnt++) printf(" <-> ");
PrintData(p->data);
p=p->next;
}
printf("<->head\n");
}
//计算链表长度
int ListLength_Du(DuLinkList L){
DuLNode *p=L->next; //p为工作指针
int cnt=0; //cnt为节点计数器
while(p!=L){ //工作指针步进并计数
p=p->next;
cnt++;
}
return cnt;
}双向循环链表的插入
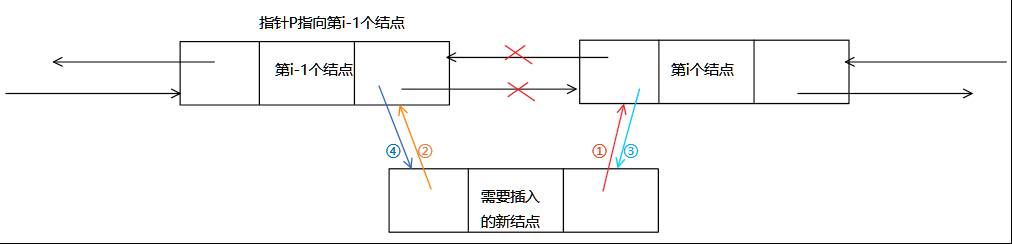
//双向循环链表的插入
bool InsertList_i_Du(DuLinkList L,int i,Elem e){
int len=ListLength_Du(L);
DuLNode *temp=(DuLNode*)malloc(sizeof(DuLNode));//为插入的元素申请结点空间
DuLNode *p=L; //工作指针
if(i>len+1||i<=0||temp==NULL)
return false; //如果链表满,或者i越界则插入失败,如果链表长Len,可以在尾部即Len+1位置上插入
temp->data=e; //结点赋值
while(--i) //找到第i-1个结点
p=p->next;
temp->next=p->next; //①新结点接管i及其之后的链表
temp->pre=p; //②新结点的前驱为i-1
p->next->pre=temp; //③原来第i个的前驱改为新结点
p->next=temp; //④将新节点勾链到i-1上
return true;
}双向循环链表的删除
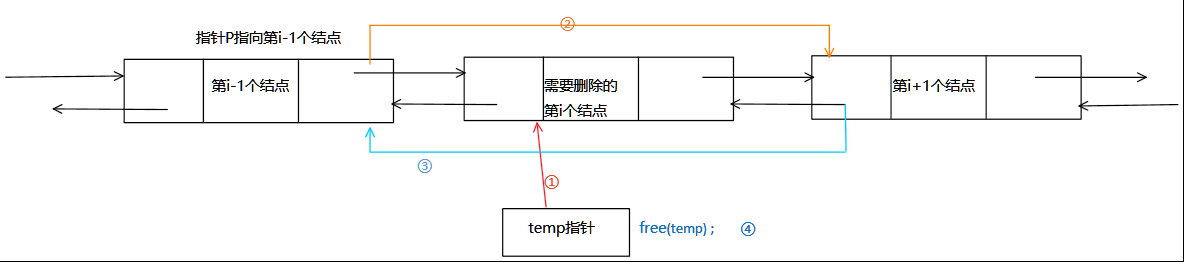
//双向循环链表的删除
bool DeleteList_i_Du(DuLinkList L,int i,Elem &e){
int len=ListLength_Du(L);
if(len==0||i>len||i<=0) //如果链表为空,或者i越界则删除失败
return false;
DuLNode* p=L; //工作指针
while(--i) //找到第i-1个结点
p=p->next;
DuLNode *temp=p->next; //①temp指向第i个结点
e=temp->data; //保存要删除的结点数据
p->next=temp->next; //②第i-1的后继为第i+1个结点
temp->next->pre=p; //③第i+1个结点的前驱为第i-1个结点
free(temp); //④释放删除的结点
return true;
}测试双向循环链表的main函数
此处用于测试的main函数调用了双向循环链表的插入和删除两个主要函数。
需要使用
std命名空间,并且包含string头文件,以便于main函数内打印分割线。int main(void){
string str="----------------------------------------------------------";
Elem temp;
//初始化并使用插入函数在第一个位置上插入结点
DuLinkList L;
InitList_Du(L);
for(int i=1;i<=10;i++){
temp.x=i;
InsertList_i_Du(L,1,temp);
}
cout<<str<<endl;
printf("链表长度:%d,链表结构如下:\n",ListLength_Du(L));
TraverseList_Du(L);
//删除第11个数据并打印删除后的链表结构
cout<<str<<endl;
printf("删除第6个结点之后,结点数据为:");
DeleteList_i_Du(L,6,temp);
PrintData(temp); putchar('\n');
printf("删除后的链表长度为:%d,链表结构如下:\n",ListLength_Du(L));
TraverseList_Du(L);
cout<<str<<endl;
return 0;
}输出结果如下:
----------------------------------------------------------
链表长度:10,链表结构如下:
head:10 <-> 9 <-> 8 <-> 7 <-> 6 <-> 5 <-> 4 <-> 3 <-> 2 <-> 1<->head
----------------------------------------------------------
删除第6个结点之后,结点数据为:5
删除后的链表长度为:9,链表结构如下:
head:10 <-> 9 <-> 8 <-> 7 <-> 6 <-> 4 <-> 3 <-> 2 <-> 1<->head
----------------------------------------------------------








Comments | NOTHING