栈和队列
栈
栈(Stack)是一种仅在表末进行插入和删除的线性表。对栈来说,表尾称为栈顶,表头称为栈底。不包含元素的空表称为空栈。
栈的ADT
//栈的ADT
ADT Stack{
数据对象:D={ai|ai ∈ Elemset , i=1,2,3...n,n>=0}
数据关系:R1={<ai-1,ai>|ai-1,ai∈D,i=2,3...n},约定an为为栈顶,a1为栈底
基本操作:
InitStack(&S)
操作结果:构造一个空的栈。
DestroyStack(&S)
初始条件:栈S已存在。
操作结果:销毁栈S的存储空间。
ClearStack(&S)
初始条件:栈S已存在。
操作结果:将S重置为空栈。
IsEmpty(S)
初始条件:栈S已存在。
操作结果:若S为空栈,返回True,否则返回false。
IsFull(S)
初始条件:栈S已存在。
操作结果:若S已满,返回True,否则返回false。
StackLength(S)
初始条件:栈S已存在。
操作结果:返回S中已经存放数据元素的个数。
GetTop(S,&e)
初始条件:栈S已存在。
操作结果:用e返回栈顶数据元素。
Push(&S,e)
初始条件:栈S已存在。
操作结果:将元素e压入栈中,成功则返回true,如果栈满打印错误信息并返回false。
Pop(&S,&e)
初始条件:栈S已存在。
操作结果:将栈顶元素出栈并赋值给e,成功则返回true,如果栈空打印错误信息并返回false。
StackTraverse(S)
初始条件:栈S已存在。
操作结果:从栈底到栈顶依次输出栈中的数据元素。
}栈的表示和实现
这里对栈的实现使用顺序结构进行实现。
//栈的定义
#define MAXSIZE 100 //栈所能容纳的最多元素个数
using namespace std;
typedef int Elem; //栈内元素类型
typedef struct SqStack{
Elem *base; //栈底指针,指向分配的连续的数组空间
Elem *top; //栈顶指针,指向栈顶元素的后一个位置
int size; //栈的大小
}SqStack;
//元素的打印函数,用于输出Elem,对数据元素的访问进行封装
void PrintData(Elem x){
printf("%d",x);
}栈的常用函数实现
//初始化栈,分配栈空间,并初始化栈顶指针
bool InitStack(SqStack &S){ //分配MAXSIZE+1个空间,栈顶指针指向栈顶元素的后一个位置
S.base=(Elem*)malloc(sizeof(Elem)*(MAXSIZE+1));
if(S.base==NULL) return false; //如果分配空间失败
S.top=S.base; //初始化栈顶指针
S.size=MAXSIZE;
return true;
}
//销毁栈,释放栈所占有的内存空间
void DestoryStack(SqStack &S){
free(S.base);
}
//清空栈,将S清除为空栈
void ClearStack(SqStack &S){
S.top=S.base; //惰性删除,直接将栈顶指针对齐到栈底
}
//判断栈空
bool IsEmpty(SqStack S){
return S.top==S.base; //如果栈顶和栈底相同,则是空栈
}
//判断栈满
bool IsFull(SqStack S){
return S.top-S.base==MAXSIZE; //如果栈顶这栈底的距离为MAXSIZE就是栈满
}
//返回栈的长度,即栈中现有的元素个数
int StackLength(SqStack S){
return S.top-S.base;
}
//读取栈顶元素,并用e返回
void GetTop(SqStack S,Elem &e){
if(IsEmpty(S)){ //如果栈空,打印错误信息并返回
printf("Stack is empty!\n");
return;
}
e=*(S.top-1); //top指向栈顶元素的后一个位置,因此-1 取元素
}
//入栈
bool Push(SqStack &S,Elem e){
if(IsFull(S)){ //如果栈满,无法入栈,打印错误信息
printf("Stack is full!\n");
return false;
}
*S.top++=e; //栈顶指针的位置进行填装,然后栈顶指针后移
return true;
}
//出栈
bool Pop(SqStack &S,Elem &e){
if(IsEmpty(S)){ //如果栈空,无法出栈,打印错误信息
printf("Stack is empty!\n");
return false;
}
e=*--S.top; //因为top指向栈顶元素的后一个位置,先将top减一,再读取栈顶的元素
}
//从栈底到栈顶依次输出栈中元素
void StackTraverse(SqStack S){
printf("栈中元素个数:%d,栈底到栈顶元素依次为:\n栈底 ",StackLength(S));
for(Elem *p=S.base;p!=S.top;p++){
PrintData(*p); putchar(' ');
}
printf("栈顶\n");
}用于测试栈的main函数
int main(void){
Elem temp;
SqStack S;
printf("-------------------------------------\n");
printf("初始化栈,把0-25压入栈中.\n");
InitStack(S);
for(int i=0;i<=25;i++){
temp=i;
Push(S,temp);
}
StackTraverse(S);
printf("-------------------------------------\n");
printf("读取并打印栈顶元素:");
GetTop(S,temp);
PrintData(temp); putchar('\n');
printf("-------------------------------------\n");
printf("出栈并打印出栈元素:");
Pop(S,temp);
PrintData(temp); putchar('\n');
StackTraverse(S);
printf("-------------------------------------\n");
printf("空栈出栈测试:");
ClearStack(S);
Pop(S,temp);
printf("-------------------------------------\n");
printf("满栈入栈测试:");
for(int i=0;i<101;i++){
temp=i;
Push(S,temp);
}
printf("-------------------------------------\n");
return 0;
}测试结果:
-------------------------------------
初始化栈,把0-25压入栈中.
栈中元素个数:26,栈底到栈顶元素依次为:
栈底 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 栈顶
-------------------------------------
读取并打印栈顶元素:25
-------------------------------------
出栈并打印出栈元素:25
栈中元素个数:25,栈底到栈顶元素依次为:
栈底 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 栈顶
-------------------------------------
空栈出栈测试:Stack is empty!
-------------------------------------
满栈入栈测试:Stack is full!
-------------------------------------栈的应用
使用栈进行括号的匹配
一个算术表达式中包含() [] {}
//这里直接使用了C++的stl中的stack,为了使得代码更加简短,并且可以直接复制使用
//需要包含stack头文件
#include<iostream>
#include<stack>
#include<string>
using namespace std;
bool BracketCheck(string str){
stack<char> s;
int i=0;
while(i<str.size()){
if(s.empty()){
s.push(str[i++]); continue; //如果是[])))这种情况中间可能遇到栈空,所以加此特判
}
switch(str[i]){
case '{':
case '[':
case '(': s.push(str[i]); break; //左括号则入栈
case '}': if(s.top()!='{') return false; //如果是右括号则和栈顶元素进行匹配,如果不匹配返回false
s.pop();break; //如果匹配,则出栈并继续循环
case ']': if(s.top()!='[') return false;
s.pop();break;
case ')': if(s.top()!='(') return false;
s.pop();break;
default : break;
}
i++;
}
if(s.empty()) return true; //如果字符串遍历完毕后栈中没有剩余,则说明匹配
else return false; //如果有剩余,则说明不匹配
}
int main(void){
string str;
cout<<"请输入一串带括号的表达式,进行表达式括号匹配的检测(输入q 结束):";
while(1){
cin>>str;
if(str=="q") break;
if(BracketCheck(str)) cout<<"括号匹配!"<<endl;
else cout<<"括号不匹配!"<<endl;
cout<<"请继续输入要进行括号匹配检测的表达式(输入q 结束):";
}
cout<<"Bye!";
return 0;
}运行可测试结果:
请输入一串带括号的表达式,进行表达式括号匹配的检测(输入q 结束):(){}[]
括号匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):{{{}}}((([[[]]])))
括号匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):{{()[]
括号不匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):()[]]]
括号不匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):(3+1)
括号匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):(4+6]
括号不匹配!
请继续输入要进行括号匹配检测的表达式(输入q 结束):q
Bye!栈的知识点补充
栈的性质
1.栈的出栈和入栈
由于栈的操作方式,如果已知入栈序列和出栈序列,则对于出栈序列来说,某个元素之前的只能是在其之前进栈的元素。
【例题】:
如果已知入栈序列是1,2,3,4,5...n,出栈序列为p1,p2,p3...pn;若p2=3,则p1可能是1和2,因为在3后边的元素不可能比3更早出栈。
2.进出栈的序列个数
n个不同的元素进栈,出栈序列的个数为:
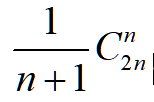









Comments | NOTHING