图的总结
图是基础数据结构中比较复杂的类型,图与二叉树不同,既有有向图也有无向图,因此其表示和相关的算法都比较复杂。在此,就图的基本表示方法和相关算法做相应的总结如下,以回顾图的相关知识,并结合自己的PAT的刷题过程记录经典的算法。
图的表示
图的表示方法有邻接矩阵、邻接表、邻接多重表,十字链表等多种表示方法,这里仅以最基础的邻接矩阵和邻接表法的表示为例。
图的表示中需要用到二维数组和相应的容器,比如邻接表的表示方法需要用到vector容器构建一个边长的二维数组用于表示邻接表。其次图的基本信息也需要另外表示,可以使用封装的方法,将有关图的所有信息封装到一个结构体中,在此,使用全局变量的方式来表示图的顶点个数和边的个数。因此,需要包含相应的头文件,并且声明相应的全局变量如下:
#include<vector> //包含vector容器的头文件
#define MAXV 1000 //图的最大顶点个数
int n,m; //图的顶点个数n 和边的条数 m图的邻接矩阵表示
图的邻接矩阵表示方法,很容易理解,使用二维的矩阵中的G[i][j]
邻接矩阵的表示有一下性质和特征:
一、对于无向图来说,由于边没有方向,故二维数组构成的矩阵是对称矩阵,因此在储存的时候可以考虑压缩存储。
二、第i行的非0或者非无穷大的权值个数即为i号顶点的出度。
三、邻接矩阵用于存放稠密图时比较合算,稀疏图的存储会导致很多空间的浪费,但是考虑到遍历的时间复杂度,邻接矩阵适合存储顶点个数较少的图,一般就PAT的测试所规定的时间来说,1000个顶点以下或者严格一点的时间限制(500个顶点以下)可以考虑采用邻接矩阵的方法表示图。
邻接矩阵的表示如下:
#define MAXV 1000 //1000个顶点以下可以考虑使用邻接矩阵存储
#define INF 0x3fffffff //用一个很大的数表示无穷大,用于表示不连通
int G[MAXV][MAXV]; //假定图的边权值为int类型邻接表的初始化:
#include<algorithm> //stl的函数模板中的fill函数用于初始化图
//方法一
int G[MAXV][MAXV]={0}; //在定义二维数组时直接全部初始化为0
//方法二
fill(G[0],G[0]+MAXV*MAXV,INF); //使用fill函数将整个数组全部初始化为无穷大,这里的参数需要使用G[0],而不是G,否则会数组越界。(这里涉及到二维数组的指针的解引用知识点)图的邻接表表示
图的邻接表表示法的基本思路是:有一个由顶点构成的顺序表(顶点表),每个顶点对应着一个链表(边表),链表中存放和自己相连接的边的相关信息。
邻接表的表示也可以分为简单版本和稍微复杂的版本:
一,简单点的只需要在边表中表示该边所连接的另一个顶点的编号即可,这种情况下可以使用变长的二维数组进行表示,顶点表为一个固定的维度,另一个维度的边表,都是变长的二维数组。示例如下:
vector<int> Adj[n]; //代表有MAXV个int型的变长数组
//数据的读入:
//1 3 //以此为例,有一条从1号顶点指向3号顶点的边
cin>>i>>j;
Adj[i].push_back(j); //有向图只需这一句,记录这条有向边即可
Adj[j].push_back(i); //如果是无向图的表示,需要i和j的边表中都加入这条边二,复杂一点的需要加入变得权值。此时需要定义编辑边结点,其中包含边的指向信息和边的权值。示例如下:
typedef struct edg{ //定义边结点
int v; //v表示该边指向的顶点的编号
int w; //w表示该边的权值
edg(int _v,int _w):v(_v),w(_w){} //边结点的构造函数,可以直接用语句edg(1,3);初始化一条边
}Edg;
vector<Edg> Adj[n]; //邻接表的定义,包含了n个顶点
//数据的读入
//1 3 12 //以此为例,一条从1号顶点指向3号顶点权值为12的边
Edg temp;
int i;
//有向图的读入
cin>>i>>temp.v>>temp.w;
Adj[i].push_back(temp);
//无向图的读入
int i,j,w;
cin>>i>>j>>w; //通过调用构造函数直接插入边节点
Adj[i].push_back(edg(j,w)); //i的边表中插入
Adj[j].push_back(edg(i.w)); //j的边表中插入图的遍历
图的遍历有深度优先和广度优先两种:深度优先遍历(DFS)和广度优先遍历。
深度优先(DFS)
深度优先:深度优先遍历采用递归的思想,对一个起始顶点开始,访问它的所有未被访问的相邻结点,对这些相邻顶点进行递归的深度优先遍历。
算法的实现:1.DFS,从一个顶点开始,遍历它的所有未被访问的相邻节点,并递归进行DFS;2.由于图可能不是连通的,有多个连通分量,因此需要一个驱动函数DFSTrave保证每一个顶点都进行一遍DFS,以保证所有的连通分量都被访问到。其伪代码如下:
DFS(int u){ //DFS函数
vis[u]=true; //用数组vis记录结点是否被访问
for(从u出发所能到达的所有顶点v){ //枚举所有u能到达的顶点v
if(vis[v]==false){ //如果未被访问,递归进行访问
DFS(v);
}
}
}
DFSTrave(G){ //DFS的驱动函数
for(G的所有顶点u){ //对每一个连通分量都进行DFS遍历
if(vis[u]==false){
DFS(u)
}
}
}对于不同的图的表示方法,DFS的写法上有所不同,但是都算法的思路都如伪代码所示,其中邻接矩阵和邻接表的写法分别如下:
DFS的邻接矩阵写法
邻接矩阵中能否到达,在这里以INF作为判定条件,假定此处使用的是带权值的图,如果G[i][j]==INF
//DFS的邻接矩阵写法
int G[MAXV][MAXV]; //邻接矩阵存储图
int n; //图的顶点个数
bool vis[MAXV]={false}; //用于标记等点是否被访问过,初始化为false
void DFS(int u,int depth){ //DFS,添加了depth参数,用于记录遍历的顶点所在的层数
vis[u]=true; //标记当前访问的顶点为已访问
visit(u); //此为访问函数,视实际需求而定
for(int v=0;v<n;v++){ //枚举所有顶点中与u相邻的顶点
if(vis[v]==false&&G[u][v]!=INF){ //如果未被访问过,且可到达
DFS(v,depth+1); //递归访问
}
}
}
void DFSTrave(){ //DFS驱动函数
for(int i=0;i<n;i++){
if(vis[i]==false){ //每一个连通分量的第一个顶点深度都从1开始计算
DFS(i,1);
}
}
}DFS的邻接表写法
邻接表的表示中,i号顶点的边表中边连接的顶点都是i可达到的,因此相比于邻接矩阵的写法,不需要判定是否能到达。因此只有图的表示和顶点枚举的写法上有所不同,其他都相同:
//DFS的邻接表写法
vector<int> Adj[MAXV]; //邻接表存储图,此没有边权
int n; //图的顶点个数
bool vis[MAXV]={false}; //用于标记等点是否被访问过,初始化为false
void DFS(int u,int depth){ //DFS,添加了depth参数,用于记录遍历的顶点所在的层数
vis[u]=true; //标记当前访问的顶点为已访问
visit(u); //此为访问函数,视实际需求而定
for(int i=0;i<Adj[u].size();i++){ //枚举u的边表中每一条边
int v=Adj[u][i]; //读取边所连通的顶点
if(vis[v]==false){ //如果未被访问过,由于邻接表中记录的都是连通的顶点,因此不用判定是否可以到达
DFS(v,depth+1); //递归访问
}
}
}
void DFSTrave(){ //DFS驱动函数
for(int i=0;i<n;i++){
if(vis[i]==false){ //每一个连通分量的第一个顶点深度都从1开始计算
DFS(i,1);
}
}
}广度优先(BFS)
广度优先:广度优先遍历与树的层次遍历类似,借用一个队列,将起顶点入队,每次从队列中弹出一个顶点,将该顶点的所有相邻顶点全部遍历一遍,并将它们依此入队,循环至队空。
算法思想,使用队列实现广度优先遍历,同样考虑到多个连通分量的情况,除了BFS还需要一个BFS的驱动函数,其伪代码如下:
BFS(u){
queue q;
q.push(u); //起始顶点入队并标记
vis[u]=ture;
while(队列q不空){
取出队首元素u进行访问;
for(从U出发可达到的所有顶点v){
if(vis[v]==false){ //如果v未曾加入过队列,入队并标记
将v入队;
vis[v]=ture;
}
}
}
}
BFSTrave(G){
for(G的所有顶点u,依此访问){
if(vis[u]==false){
BFS(u);
}
}
} BFS的邻接矩阵写法
与DFS相类似的,只需要针对不同的表示方法,写出不同的类型的枚举语句即可:
//BFS邻接矩阵写法
int n,G[MAXV][MAXV]; //n为顶点数,G为邻接矩阵
bool vis[MAXV]={false}; //是否在队列的标记数组,初始化为false
void BFS(int u){
queue<int> q; //起始顶点入队
q.push(u);
vis[u]=true; //标记并访问
while(!q.empty()){ //当队不空时进行循环
int u=q.front(); //取出队头元素u
q.pop();
visit(u); //访问函数,视实际需求而定
for(int v=0;v<n;v++){ //枚举u所有的未访问且可到达顶点
if(vis[v]==false&&G[u][v]!=INF){
q.push(v); //入队并修改访问标记
vis[v]=true;
}
}
}
}
void BFSTrave(){ //BFS的驱动函数
for(int u=0;u<n;u++){
if(vis[u]==false){
BFS(u);
}
}
}BFS的邻接表写法
BFS的邻接表写法和邻接矩阵的写法只在图的表示和枚举的表示上有所不同,代码如下:
//BFS邻接表写法
vector<int> Adj[MAXV]; //图的不带边权邻接表表示
int n; //n为顶点数
bool vis[MAXV]={false}; //是否在队列的标记数组,初始化为false
void BFS(int u){
queue<int> q; //起始顶点入队
q.push(u);
vis[u]=true; //标记并访问
while(!q.empty()){ //当队不空时进行循环
int u=q.front(); //取出队头元素u
q.pop();
visit(u); //访问函数,视实际需求而定
for(int i=0;i<Adj[u].size();i++){ //枚举u边表中的所有边
int v=Adj[u][i]; //读取边所连通的所有顶点
if(vis[v]==false){ //如果未被访问
q.push(v); //入队并修改访问标记
vis[v]=true;
}
}
}
}
void BFSTrave(){ //BFS的驱动函数
for(int u=0;u<n;u++){
if(vis[u]==false){
BFS(u);
}
}
}BFS和层数
BFS可以类比于DFS的做法,增加一个新的参数,用于记录遍历的层数,例如,起始顶点的层数记为第0层,其伪代码如下所示:
//BFS与层数
BFS(u){
queue q;
q.push(u);
vis[u]=ture;
int level=0,last=u; //layer表示层数,起始顶点为0层,last表示当前层的最后一个,用于判断是否该层结束,初始化为起始顶点u
int tail=u; //tail用于跟踪当前顶点u的下一层顶点,该层结束后,变成该层的最后一个,用于更新last的值
while(队列q不空){
取出队首元素u进行访问;
for(从U出发可达到的所有顶点v){
if(vis[v]==false){ //如果v未曾加入过队列,入队并标记
将v入队;
vis[v]=ture;
tali=v;
}
}
if(u==last){
level++; //当前层结束,层数加一,统计进入下一层
last=tail; //last更新为新一层的最后一个
}
}
} 小结
遍历的小结:
1.图的遍历过程中如果需要访问只需在修改访问标记的语句vis[u]=true
2.其中,如果为了方便访问标记数组和图的遍历和修改,可以直接定义为全局变量。更加严谨安全的做法,应该是定义成主函数中的局部变量,然后各个函数根据数据规模分别传指针或者传引用。
3.图的遍历也可以用于判断图是否连通,在驱动函数处加入计数器,统计连通分量的个数即可。
4.图的遍历根据实际情况根据实际的需求加入相应的判定形成特殊的递归边界,以实现递归的剪纸,以优化运行速度或者避免不需要的递归访问。
最短路径
最短路径的求解问题,主要包含两种:单源最短路径和多源路径最短问题。求单源最短路径的算法主要有Dijkstra算法,以及多尺度优化条件的Dijkstra算法,还有使用Dijkstra+DFS求解单源最短路径的算法;求解多源最短路径的算法,这里仅给出算法思想相对简单的Floyd算法代码。
单源最短路径(Dijkstra算法)
Dijkstra算法用于求解给定图G和给定起始顶点s,求s到其他各个顶点的最短距离。Dijkstra算法的策略是:
1.设置集合S,存放已被访问的顶点集。
2.然后从未被访问过的顶点集中选择到达S集合的最短距离的顶点u,加入到S中。
3.以u为中介点,更新顶点集S到剩余未访问的顶点的距离。
4.循环直到连通分量的所有顶点都被收录。
算法的实现
算法的具体实现方法:
1.首先需要一个bool型数组vis记录是否被加入顶点集S;2.然后需要一个dis数组记录起始顶点s到所有其他顶点的最小距离。3.如果有需要记录最短路径,还需要有记录路径的数组path。其伪代码如下所示:
//G表示图,可使用全局变量,数组dis表示从起始顶点到其他顶点的最短路径
Dijkstra(G,dis[],s){
初始化; //初始化dis数组为无穷大,并将起点s的dis初始为0;
for(循环n次){
u=使dis[u]最小的还未被访问的顶点的编号
记u被访问;
for(从u出发所能到达的所有顶点v){
if(v未被访问&&以u为中介点使s到v的最短距离dis[v]更优){
优化dis[v];
}
}
}
} Dijkstra算法针对不同的图的表示方法,写法上只有枚举和判定是否能到达这两点上有所不同。
Dijkstra算法的邻接矩阵写法:
//Dijkstra算法的邻接矩阵写法
int n,G[MAXV][MAXV]; //图的顶点个数和邻接矩阵表示
int dis[MAXV]; //记录距离的数组
bool vis[MAXV]={false}; //访问标记数组
void Dijkstra(int s){ //参数为单源起点s
fill(dis,dis+MAXV,INF); //初始化dis数组为无穷大
dis[s]=0; //起始顶点s到自身的距离为0
for(int i=0;i<n;i++){ //执行n次循环,每次把一个新的顶点纳入顶点集S
int u=-1,MIN=INF; //u使得dis[u]最小,并用MIN记录dis[u]
for(int j=0;j<n;j++){
if(vis[j]==false&&dis[j]<MIN){
u=j;
MIN=dis[j];
}
}
if(u==-1) return; //如果找不到这样的u,说明不连通或者已经遍历结束,则返回
vis[u]=true; //标记u为已访问
for(int v=0;v<n;v++){ //对u能到达的顶点v进行优化
if(vis[v]==false&&G[u][v]!=INF&&dis[u]+G[u][v]<dis[v]){
dis[v]=dis[u]+G[u][v];
}
}
}
}Dijkstra算法的邻接表写法:
//Dijkstra算法的邻接表写法
typedef struct egd{ //邻接表边结点的结构体定义
int v; //v为边的目标顶点,d为边的权值
int d;
}Edg;
int n; //图的顶点个数和邻接表
vector<Edg> Adj[MAXV];
int dis[MAXV]; //记录距离的数组
bool vis[MAXV]={false}; //访问标记数组,初始化全为否
void Dijkstra(int s){ //参数为单源起点s
fill(dis,dis+MAXV,INF); //初始化dis数组为无穷大
dis[s]=0; //起始顶点s到自身的距离为0
for(int i=0;i<n;i++){ //执行n次循环,每次把一个新的顶点纳入顶点集S
int u=-1,MIN=INF; //u使得dis[u]最小,并用MIN记录dis[u]
for(int j=0;j<n;j++){
if(vis[j]==false&&dis[j]<MIN){
u=j;
MIN=dis[j];
}
}
if(u==-1) return; //如果找不到这样的u,说明不连通或者已经遍历结束,则返回
vis[u]=true; //标记u为已访问
//只有这里的for循环和邻接矩阵的写法有所不同
for(int j=0;j<Adj[u].size();j++){ //对u能到达的顶点v进行优化
int v=Adj[u][j].v;
if(vis[v]==falsed&&is[u]+Adj[u][j].d<dis[v]){
dis[v]=dis[u]+Adj[u][j].d;
}
}
}
}算法的扩展应用
在Dijkstra算法的基础上,进行相应的扩展,比如:求解并输出最短路径上的结点、根据不同的优化尺度进行优化的选择、Dijkstra+DFS的等等。
1.记录最短路径
实现方法:使用一个path数组记录每次优化时,优化的结点的前驱结点,然后从最短路径的重点开始递归读取path数组获得路径,或者使用栈的方式,入栈再出栈,将倒着找到的最短路径顺序输出。伪代码如下:
if(v未被访问&&以u为中介点使s到v的最短距离dis[v]更优){
优化dis[v];
令v的前驱结点为u;
}这里以邻接矩阵的实现为举例:
//Dijkstra算法的邻接矩阵写法(带路径)
int n,G[MAXV][MAXV]; //图的顶点个数和邻接矩阵表示
int dis[MAXV]; //记录距离的数组
bool vis[MAXV]={false}; //访问标记数组
int path[MAXV]; //(新)记录路径的数组,path[v]记录最短路径上v的前驱顶点
void Dijkstra(int s){ //参数为单源起点s
fill(dis,dis+MAXV,INF); //初始化dis数组为无穷大
fill(path,path+MAXV,-1) //(新)路径数组初始化前驱节点-1
dis[s]=0; //起始顶点s到自身的距离为0
for(int i=0;i<n;i++){ //执行n次循环,每次把一个新的顶点纳入顶点集S
int u=-1,MIN=INF; //u使得dis[u]最小,并用MIN记录dis[u]
for(int j=0;j<n;j++){
if(vis[j]==false&&dis[j]<MIN){
u=j;
MIN=dis[j];
}
}
if(u==-1) return; //如果找不到这样的u,说明不连通或者已经遍历结束,则返回
vis[u]=true; //标记u为已访问
for(int v=0;v<n;v++){ //对u能到达的顶点v进行优化
if(vis[v]==false&&G[u][v]!=INF&&dis[u]+G[u][v]<dis[v]){
dis[v]=dis[u]+G[u][v];
path[v]=u; //(新)如果进行了优化,则记录v的前驱顶点为u
}
}
}
}
//输出最短路径
void Print_Path(int s,int v){ //s为起始顶点,v为最短路径的终点
vector<int> pathout; //定义用于输出的栈,pathout,这里使用vector模拟栈的使用
while(v!=-1){ //递归入栈
pathout.push_back(v);
v=path[v];
}
for(int i=pathout.size()-1;i>=0;i--){ //栈中路径倒序输出
cout<<pathout[i]<<' ';
}
}
2.多尺度优化
①新增边权:边权有两个,一个代表距离花费,一个代表时间花费。这是需要增加另外记录时间花费,比如新开二维数组cost[u][v]记录时间花费,然后新增数组c[]
int G[MAXV][MAXV]; //图的距离权值
int cost[MAXV][MAXV]; //图的时间花费权值
//最短距离和最短时间,除起始顶点自身初始化为0以外,其他全部初始化为INF
int dis[MAXV]; //最短距离数组
int c[MAXV]; //最短花费数组
//优化代码
for(int v=0;v<n;v++){
if(vis[v]==false&&G[u][v]!=INF){ //u的可到达未访问顶点
if(dis[u]+G[u][v]<dis[v]){
dis[v]=dis[u]+G[u][v];
c[v]=c[u]+cost[u][v]; //距离最优时,同时优化距离和时间
}
else if(dis[u]+G[u][v]==dis[v]&&c[u]+cost[u][v]<c[v]){
c[v]=c[u]+cost[u][v]; //距离相同时,看时间是否最优
}
}
} ②新增点权:对于新增点权的情况来说,一般顶点的权值代表了顶点的资源多少,这时需要增加一个weight[]
int G[MAXV][MAXV]; //图的距离权值
int weight[MAXV]; //顶点的资源权值,
//最短距离和最短时间,除起始顶点自身初始化为0以外,其他全部初始化为INF
int dis[MAXV]; //最短距离数组
int w[MAXV]; //w[u]表示从起始顶点开始到达顶点u能够收集到的资源
//w数组中除了起始顶点初始化为自身顶点的资源weight[s]以外,其他顶点都初始化为0
//优化代码
for(int v=0;v<n;v++){
if(vis[v]==false&&G[u][v]!=INF){ //u的可到达未访问顶点
if(dis[u]+G[u][v]<dis[v]){
dis[v]=dis[u]+G[u][v];
w[v]=w[u]+weight[v]; //距离最优时,同时优化距离和资源
}
else if(dis[u]+G[u][v]==dis[v]&&w[u]+weight[u][v]>w[v]){
w[v]=w[u]+weight[v]; //距离相同时,看资源能够更优,这里以能够带更多的资源为更优
}
}
} ③求最短路径的条数:统计路径条数,只需要另外增加一个记录路径条数的数组num[]即可,用num[u]表示从起始顶点s到顶点u之间的路径条数,其中num[s]初始化为1,其他初始化为0,然后在更新路径时,如果以u为中介点可以使s到v距离更优,那么num[v]继承num[u]即可,但是如果遇到通过u为中介点使s到u的距离相同,这时把num[u]加到num[v]
int num[MAXV]; //路径条数数组,初始化起点的num[s]=1,其他初始化为0
//优化代码
for(int v=0;v<n;v++){
if(vis[v]==false&&G[u][v]!=INF){ //u的可到达未访问顶点
if(dis[u]+G[u][v]<dis[v]){
dis[v]=dis[u]+G[u][v];
num[v]=num[u]; //距离最优时,路径条数继承
}
else if(dis[u]+G[u][v]==dis[v]){
num[v]+=num[u]; //距离相同时,路径条数累加
}
}
}通用的Dijkstra+DFS求解算法
通用模板的总结:对于更加复杂的优化规则,使用如上所示的优化代码,可能逻辑上过于复杂,容易出错,因此可以采用Dijkstra+DFS算法,将所有最短路径都求解出来,然后枚举每一条路径,计算每条路径的优化尺度,然后选择最优的那一条。
算法的实现分为两个主要部分:
第一步是通用的Dijkstra算法的最短路径求解。由于有可能有多条路径,所以用于记录前驱结点的path数组需要扩展为vector类型的数组vector<int> path[MAXV],这样对于每一个顶点u来说都能在path[u]这个边长数组中存储前驱结点,但是此时path[v]
int n,G[MAXV][MAXV]; //图的顶点个数和邻接矩阵表示
int dis[MAXV]; //记录距离的数组
bool vis[MAXV]={false}; //访问标记数组
vector<int> path[MAXV]; //(新)使用边长数组记录每个顶点的前驱
void Dijkstra(int s){ //参数为单源起点s
fill(dis,dis+MAXV,INF); //初始化dis数组为无穷大
dis[s]=0; //起始顶点s到自身的距离为0
for(int i=0;i<n;i++){ //执行n次循环,每次把一个新的顶点纳入顶点集S
int u=-1,MIN=INF; //u使得dis[u]最小,并用MIN记录dis[u]
for(int j=0;j<n;j++){
if(vis[j]==false&&dis[j]<MIN){
u=j;
MIN=dis[j];
}
}
if(u==-1) return; //如果找不到这样的u,说明不连通或者已经遍历结束,则返回
vis[u]=true; //标记u为已访问
for(int v=0;v<n;v++){ //对u能到达的顶点v进行优化
if(vis[v]==false&&G[u][v]!=INF){
if(dis[u]+G[u][v]<dis[v]){ //当能够以u为中介点进行优化时
dis[v]=dis[u]+G[u][v]; //进行优化
path[v].clear(); //path中的前驱使用覆盖式更新,即先清空,后更新
path[v].push_back(u);
}
esle if(dis[u]+G[u][v]==dis[v]){
path[v].push_back(u); //当出现相同长度的路径时,采用添加式更新,不清除
}
}
}
}
}第二步,对记录的每一条路径进行DFS,然后统计第二优化尺度,选出符合要求的路径进行输出,这时候需要一个数组临时存放枚举的每一条完整的路径temppath,还需要一个保存完整的最终输出的数组pathout,然后对对Dijkstra算法生成的所有最短路径做递归的DFS遍历,获得符合要求的输出结果,代码如下:
int optvalue; //第二尺度最优值,根据实际情况进行初始化
vector<int> path[MAXV]; //保留路径上每个顶点的前驱顶点
vector<int> pathout,temppath; //保存完整的输出路径和临时的最优路径
void DFS(int v){ //v为当前访问的顶点
//递归边界
if(v==s){ //如果到达顶点,则表示已经生成了一条临时路径
temppath.push_back(s); //加入起始顶点,补全路径
int value; //临时存放第二尺度的值
计算临时路径上的第二尺度的值,例如时间花费或者顶点资源数量等(见注释);
if(value由于optvalue){ //如果是较为优化的路径,就记录给pathou和optvalue
optvalue=value;
pathout=temppath;
}
temppath.pop_back(); //将刚加入的结点删除,返回继续向另外的分支进行递归
return;
}
//递归式
temppath.push_back(v);
for(int i=0;i<path[v].size();i++){
DFS(path[v][i]);
}
temppath.pop_back(); //完成本层递归的所有遍历后,删除当前结点v返回上一层继续转向另外的分支进行递归
}
**注释:**计算临时路径上的第二尺度的值,根据实际情况选择顺序或者倒序遍历temppath数组获得!
多源最短路径(Floyd算法)
Floyd算法的思路相当简洁,对于整个图来讲,任意的顶点i和j如果存在一个中间顶点k使得顶点i到j的路径变得更短,就用k来优化i到j的路径,这样显然枚举所有的n个顶点,是他们分别作为中间顶点 优化每一对顶点之间的距离,就获得了任意两点之间的最短路径,这就是多源路径最短的Floyd算法的思想。其伪代码如下:
for(枚举所有n个顶点,然他们依此充当中间顶点k){
for(以k为中介点,枚举所有的定点对i和j,i∈[0,n-1],j∈[0,n-1]){ //此处为两重循环,遍历所有的顶点对儿
if(以k为中间顶点,使距离更优){
更新i到j的距离;
}
}
}
Floyd算法的实现代码如下:
int dis[MAXV][MAXV]; //图任意两顶点之间的距离二维数组(即图的初始状态),如果图只需要一遍处理的话,可以直接在图上执行Floyd算法
//Floyd算法
void Floyd(){
for(int k=0;k<n;k++){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(dis[i][k]!=INF&&dis[k][j]!=INF&&dis[i][k]+dis[k][j]<dis[i][j]){
dis[i][j]=dis[i][k]+dis[k][j]; //如果i,j之间可以用k做中介点,并且k使得i,j之间距离更优,则更新dis[i][j]
}
}
}
}
}小结
求解最短路径问题的时候,对于单元路径最短问题,如果只有两个尺度,而且判定不复杂的情况下,直接使用Dijkstra算法的双尺度判定优化算法;如果涉及到较多的尺度和较为复杂的判定逻辑,则使用Dijkstra+DFS的算法,对获得的所有最短路径单独进行尺度优化的判定,以获得最终需要的结果。相对来说,第一种算法简单有效,第二种算法更加通用,可根据求解题目的复杂程度进行选择。
最小生成树
最小生成树指的是在一个给定的无向图中求出一颗树,这棵树拥有图的所有顶点,并且树的边来自图中的边,且满足树的边权最小。求解最小生成树有两种方法:Prim算法和kruskal算法。
Prim算法
Prim算法类似于Dijkstra算法的过程,从起始顶点开始,将已选中的顶点归到点集S中,每次从位访问的顶点中选择离点集最近的结点,并将其纳入点集S中,执行n次循环,直到包含整个图的所有顶点。其伪代码的实现如下:
//G位图,数组dis[u]表示顶点u距离点集S的距离 dis数组的含义与Dijkstra算法是有区别的
Prim(G,dis[]){
初始化;
for(循环n次){
u=使dis[u]最小的顶点编号;
记u已被访问;
for(从u出发能访问到的顶点v){
if(v未被访问&&以u为中介点使得v到点集S的距离更优){
将G[u][v]赋值给v与点集S的最短距离d[v];
}
}
}
}由伪代码可以很容易写出邻接矩阵和邻接表表示的算法代码,这里仅给出邻接矩阵的写法,邻接表的写法只在判定条件的写法上有所不同:
//Prim算法的邻接矩阵写法
int n,G[MAXV][MAXV]; //图的顶点个数和邻接矩阵表示
int dis[MAXV]; //记录每一个顶点到点集S的距离数组,除了起始顶点初始化为0以外,其他初始化为无穷大
bool vis[MAXV]={false}; //访问标记数组
int Prim(int s){ //参数为最小生成树的根结点,即起点s,返回值为树的权值
int ans=0; //用于记录最小生成树的边权之和
fill(dis,dis+MAXV,INF); //初始化dis数组为无穷大
dis[s]=0; //起始顶点s到点集S的距离为0
for(int i=0;i<n;i++){ //执行n次循环,每次把一个新的顶点纳入顶点集S
int u=-1,MIN=INF; //u使得dis[u]最小,并用MIN记录dis[u]
for(int j=0;j<n;j++){
if(vis[j]==false&&dis[j]<MIN){
u=j;
MIN=dis[j];
}
if(u==-1) return -1; //如果找不到这样的u,说明不连通,则构不成最小生成树,返回-1;
vis[u]=true; //标记u为已访问
ans+=dis[u]; //将u加入点集S,并将其到达点集S的距离加入最小生成树
for(int v=0;v<n;v++){ //对u能到达的顶点v进行优化
if(vis[v]==false&&G[u][v]!=INF&&G[u][v]<dis[v]){
dis[v]=G[u][v]; //如果通过u能使v到达点集S的距离更优,则将u——v这条边赋值给dis[v]
}
}
}
return ans; //返回最小生成树的边权之和
}Kruskal算法
kruskal算法的思路是选边,每次从未被选中的边中选出最小的边,如果选中的边不构成回路,就加入到最小生成树中去,直到选中的边数等于顶点个数减一,即n-1的时候结束循环。其伪代码如下:
int kruskal(){
用ans记录最小生成树的边权之和,用edgnum记录以选中的边的数量;
将所有的边按权值从小到大排列;
for(从小到大枚举所有的边){
if(边的两个顶点不在同一个连通块中){ //判断是否会形成回路
将该边加入到最小生成树中;
ans+=测试边的权值;
最小生成树的边计数edgnum加一;
if(edgnum==n-1){
当已经选中n-1条边时结束循环;
}
}
}
return ans;
}实际代码的实现有两个问题,首先如何判断两个顶点是否在同一个连通块中,其次,如何将边加入到最小生成树中。解决这个问题可以使用并查集,并查集可以很容易的辨别两个点是否在同一个连通块中,同时将测试边的两个端点所在的并查集合并,就能达到将边加入到最小生成树的效果。因此,需要增加一个并查集数组,一个查询两个顶点所属的并查集的查询函数,其代码如下:
int father[N]; //并查集数组,全部初始化为-1
int find_father(int i){
while(father[i]!=-1){ //如果一个元素的父节点下标是-1,其绝对值表示该并查集的元素个数,那么这个结点便是这个并查集的根
i=father[i];
}
return i; //返回并查集的根
}
//kruskal算法
typedef struct edg{ //定义边的结构体
int st,ed; //边连接的开始顶点st和结尾顶点ed
int v; //边的权值
}Edg;
vector<Edg> edgv; //存放边的数组
bool cmp(Edg a,Edg b){
return a.v<b.v; //按照边的权值从小到大排序
}
int kruskal(int n,vector<Edg> &egdv ){ //n表示顶点个数,v传引用存放边的数组
int ans=0,edgnum=0;
fill(father,father+N,-1); //初始化并查集数组
sort(edgv.begin(),edgv.end(),cmp) //边按权值从小到大排序
for(int i=0;i<edgv.size();i++){
int fst=find_father(edgv[i].st);
int fed=find_father(edgv[i].ed);
if(fst!=fed){ //如果两个顶点不在同一个并查集,合并集合
if(father[fst]<father[fed]){ //这里为了保证并查集的合并的规模平衡,优先采用小的合并到大的并查集中
father[fst]+=father[fed];
father[fed]=fst;
}
else{
father[fed]+=father[fst];
father[fst]=fed;
}
ans+=edgv[i].v; //将该边权值计入最小生成树
edgnum++; //最小生成树的边数加一
if(edgnum==n-1) break; //当选够n-1条边时结束算法
}
}
if(edgnum!=n-1) return -1; //如果循环结束时无法连通,返回-1,无法得到最小生成树
else return ans; //返回最小生成树的边权之和
}小结
由于Kruskal算法主要的开销在于边的按权值排序,因此可知kruskal算法适用于边数较少的情况。所以,一般情况下,如果是稠密图,使用Prim算法,如果是稀疏图,则用kruskal算法。
拓扑排序
拓扑排序是有向无环图的所有顶点拍成的一个线性序列,反映了顶点在逻辑上的先后条件关系,比如先学了某几门特定的基础课程之后才能学习一门专业课程。这种序列关系可以称之为拓扑排序。
拓扑排序算法的实现
拓扑排序的算法思想是,对于某个有向无环图(DAG图)从某一个没有前驱的顶点开始(即入度为0的顶点),将它归入拓扑序列后,将它所有的边全部删除,然后继续从剩余的顶点中选出入度为0的顶点,继续循环,直到取完全部的顶点,便可以得到一个拓扑序列。显然,当入度为0的顶点不止一个的时候,选取的不同的点就会得到不同的拓扑序列,可见拓扑序列不是唯一的。
拓扑排序的实现需要记录每一个顶点的入度,以判断入度是否为0,其算法的代码实现如下:
vector<int> G[MAXV]; //使用不带权值的图的邻接表的表示方法
int n,m,indegree[MAXV]; //n表示顶点个数,m表示边的条数,indegree用于记录每个顶点的入度
bool topsort(){
int num=0; //用于统计拓扑序列中的顶点个数,如果最后不能包含全部n个顶点,说明不能得到拓扑排序,此图不是有向无环图
queue<int> q; //类似于层次遍历的方法,借助队列实现遍历所有的顶点
for(int i=0;i<n;i++){ //将所有的入度为0的顶点加入到队列中
if(indegree[i]==0){
q.push(i);
}
}
while(!q.empty()){ //读取每一个入度为0的顶点
int u=q.front();
q.pop();
printf("%d ",u ); //输出拓扑排序的顶点
for(int i=0;i<G[u].size();i++){ //然后将它的后继顶点的入度全部减一
int v=G[u][i];
indegree[v]--;
if(indegree[v]==0){ //如果顶点入度变成了0,也入队
q.push(v);
}
}
num++; //拓扑排序中的顶点个数加一
}
if(num==n) return true; //如果能够得到拓扑排序返回真
else return false; //否则说明无法生成拓扑排序,此图不是有向无环图
}关键路径
AOE网与AOV网
顶点活动(AOV)网表示用顶点代表活动,用边代表活动优先顺序的有向图关系。边活动(AOE)网指的是用带权的边表示活动,用顶点表示时间的有向图,这时候有权边表示了活动的时间花费。
一般来说,一个工程可以用一个AOE网表示其进程,工程长分为若干子工程,显然AOE网不能有环,否则会出现,环内的所有定点都是其他顶点的先决条件,这将导致整个工程无法完成。对于AOV网来说有类似的逻辑关系。
AOE网中,可能有多个源点(活动的起始顶点)或者多个汇点(活动结束的点),这种情况下可以采用给多个源点添加一个统一的源点——“超级源点”,或者给多个汇点添加一个统一的汇点——“超级汇点”的方法转化为一个源点和一个汇点的情况,如下图所示:
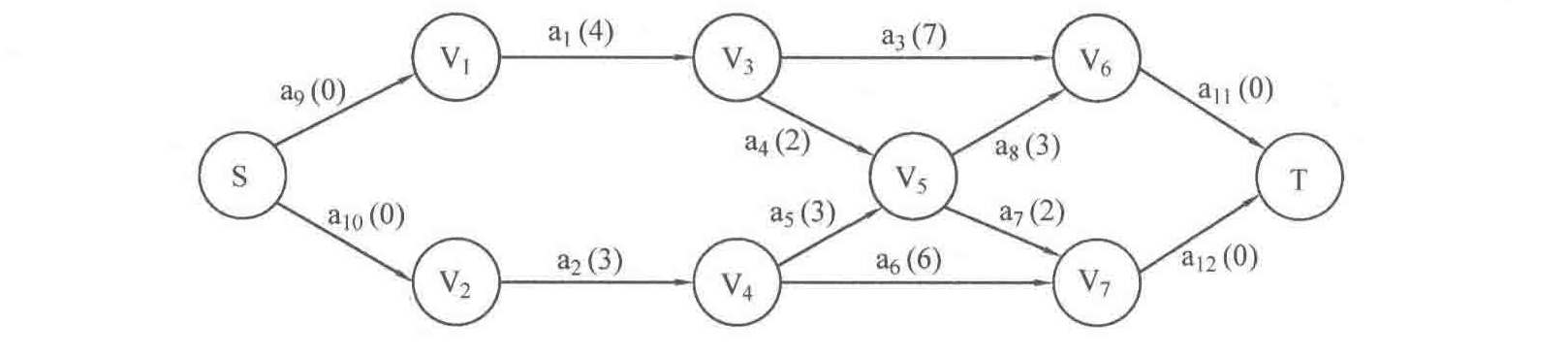
AOV网,可以将一个顶点事件拆分为两个顶点,分别为该事件的起始和结束,边表示该事件的时间花费,如下所示的方法,将AOV网转化为AOE网的样子:
AOE网:
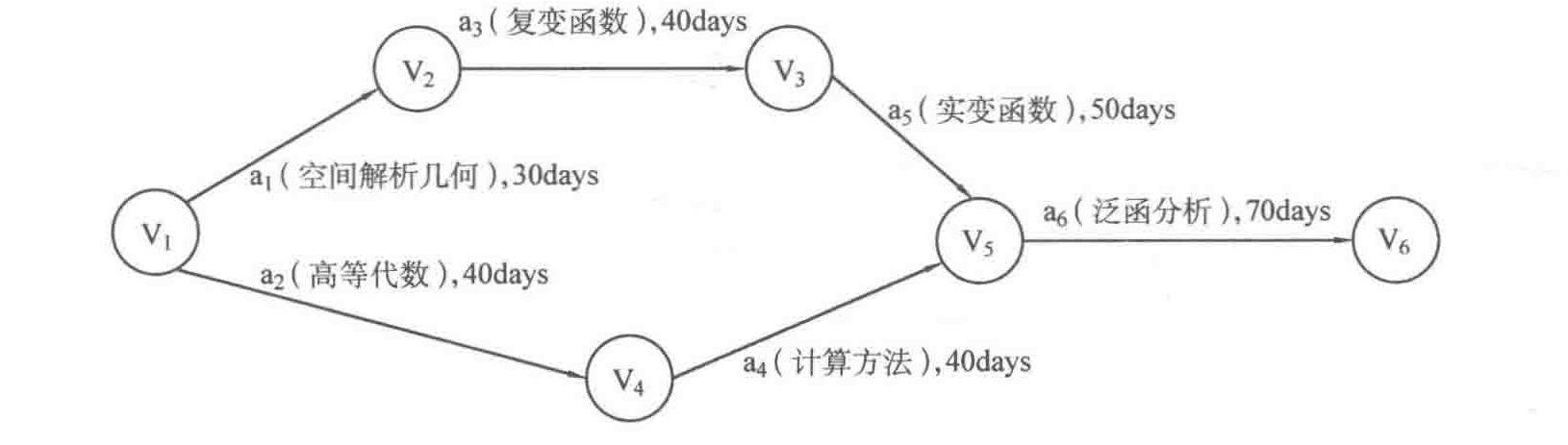
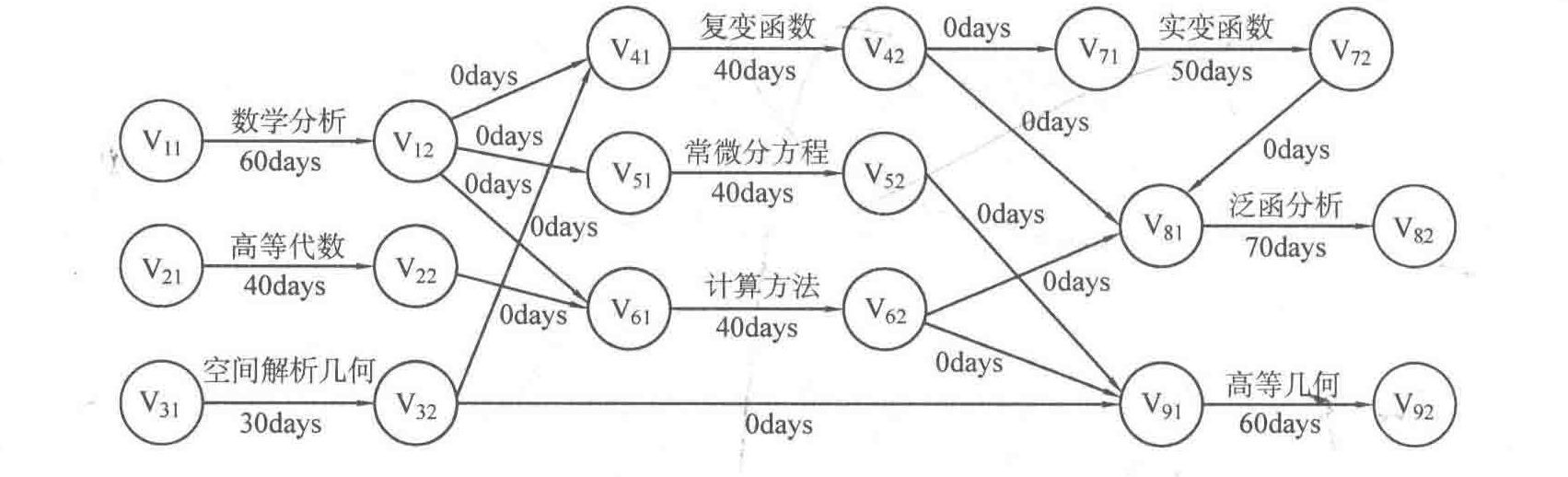
AOE转化成AOV网:
关键路径的求解思路
基于拓扑排序的关键路径求解
AOE网实际上是邮箱无环图,关键路径是图中的最长路径,这里给出求解有向无环图(DAG)的最长路径的求解思路:

由于关键活动没有时间余量,不允许拖延,因此这些轰动的最早开始时间必须等于最迟开始时间,这里用数组e和l分别记录每一个活动的最早开始和最迟开始时间,对于活动ar来说,e[r]和l[r]表示了活动的最早开始时间和最迟开始时间,如果对于活动ar有e[r]==l[r],那么这个活动便不允许拖延,就是关键路径。
但是求解e和l数组需要借助活动ar两端的事件,如果用ve和vl数组表示顶点事件的最早和最迟发生时间那么有以下关系:
①ar的最早发生时间是事件Vi的最早发生时间,即e[r]=ve[i];
②ar的最迟发生事件是事件Vj的最迟发生时间减去活动ar的时间花费,即l[r]=vl[j]-length[r];
一、求解ve
由此可见,只需要求出ve和vl就可以求出活动的e和l。对于ve数组的求解来说,计算某个事件Vj,如果事件Vj有很多前置事件,例如有k个事件Vi1~ Vik那么显示必须所有的前置事件完成后才能开始事件Vj,因此Vj的最早开始事件为前置事件中ve[i1]+lengh[r1]~ve[ik]+lengh[rk]的最大值。可理解如下:
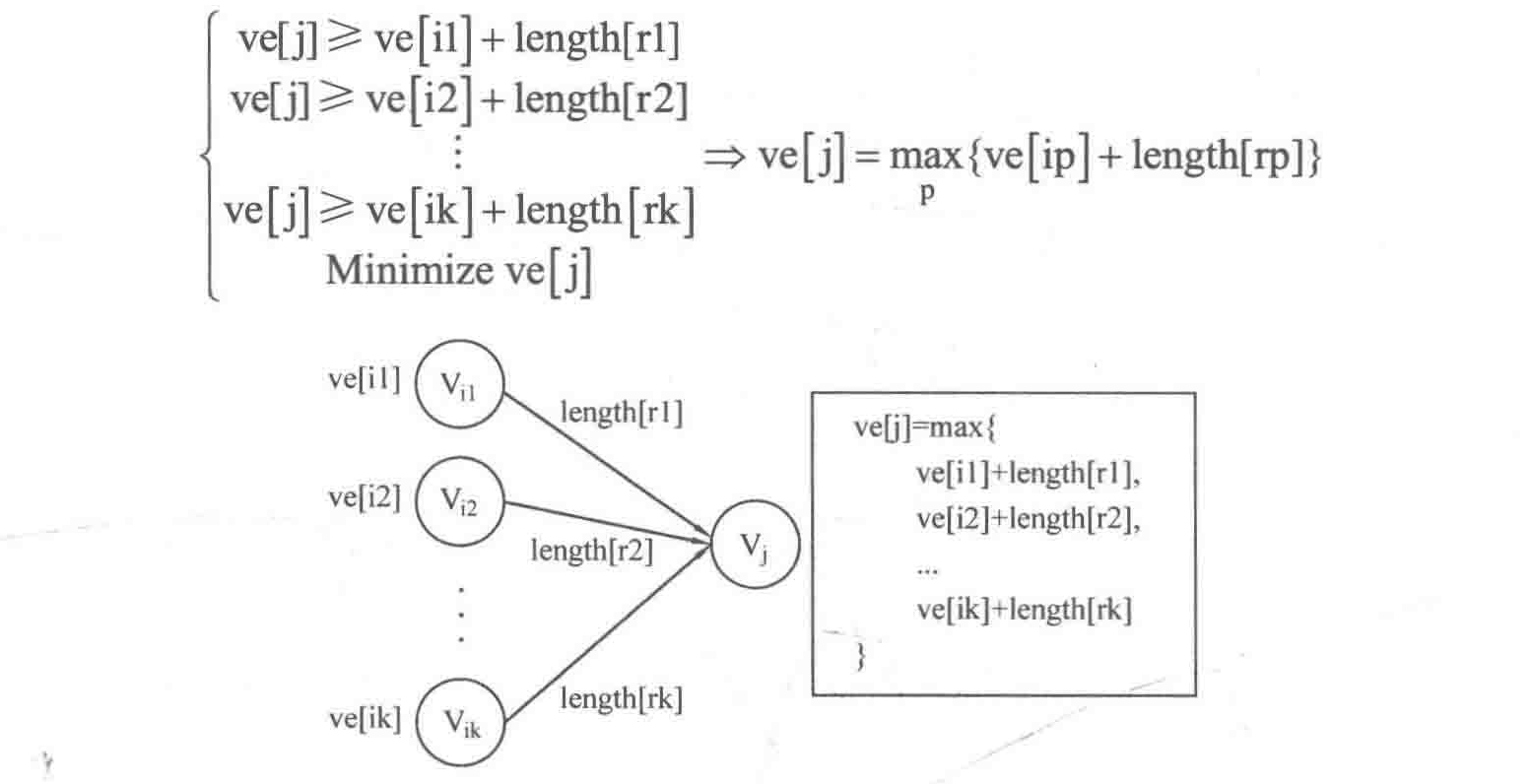
显然,想要球的ve[j]就必须直到前置事件的ve,这里借助拓扑排序来实现,这样保证了遇到事件Vj的时候,所有的前置事件的ve已全部求出,只需找到ve[i1]+lengh[r1]~ve[ik]+lengh[rk]的最大值即可,代码实现如下所示:
//图以及求解关键路径时使用的容器的定义和声明
typedef struct { //活动结点
int st,ed; //活动的开始事件顶点和结束事件顶点
int e,l; //活动的最早开始时间和最晚开始时间
int id,len; //活动的编号和活动的花费
}Act;
int n,m; //图的顶点个数和边数
int G[MAXV][MAXV]; //记录图
int inDegree[MAXV]={0}; //结点的入度数组
vector<Act> v; //记录边的容器
int ve[MAXV]={0}, vl[MAXV]; //活动的最早开始时间和最晚开始时间,ve
初始化为0,vl初始化为关键路径长度
stack<int> toporder; //存放拓扑序列 //利用拓扑排序实现ve数组的求解
int topsort() //拓扑排序
{
queue<int> q;
for(int i=1;i<=n;i++){ //把所有入度为0顶点的入队
if(inDegree[i]==0){
q.push(i);
}
}
int u;
int maxlen=0; //记录最大的ve 就是整个工程的最短时间
while(!q.empty()){
u=q.front(); //从队列中取出一个结点
q.pop();
toporder.push(u);
for(int i=1;i<=n;i++){ // 将他的后继结点的入度减一
if(G[u][i]!=INF){
inDegree[i]--;
if(inDegree[i]==0) //如果入度也变为0,入队
q.push(i);
//更新u的后序结点的ve值
if(ve[u]+G[u][i]>ve[i]){
ve[i]=ve[u]+G[u][i];
if(ve[i]>maxlen) //更新过后,寻找最短时间,即关键路径的长度
maxlen=ve[i]; //关键路径长度等于汇点活动的最早开始时间的最大值
}
}
}
}
if(toporder.size()==n) return maxlen; //如果是有向无环图,返回关键路径的长度vl求解函数用于初始化vl数组
else return -1; //否则返回-1,表示图中有环,整个工程调度不可行
} 以上算法不仅能够通过返回值得到关键路径的长度,还能判断是否是有向无环图,由此判断工程调度是否合理。
二、求解vl数组
vl数组的求解,对于事件Vi来说,其vl的值需要通过其后继的事件推出,显然如果事件Vi的后继有k个事件Vj1~ Vjk分别由权值为length[r1]~length[rk]的活动边r1~rk连接,则事件Vi的最迟发生时间为vl[j1]-length[r1]~vl[jk]-length[rk]的最小值,选最小值的原因是为了保证后继事件的最迟发生时间得到保障,可以通过下面的公式理解:
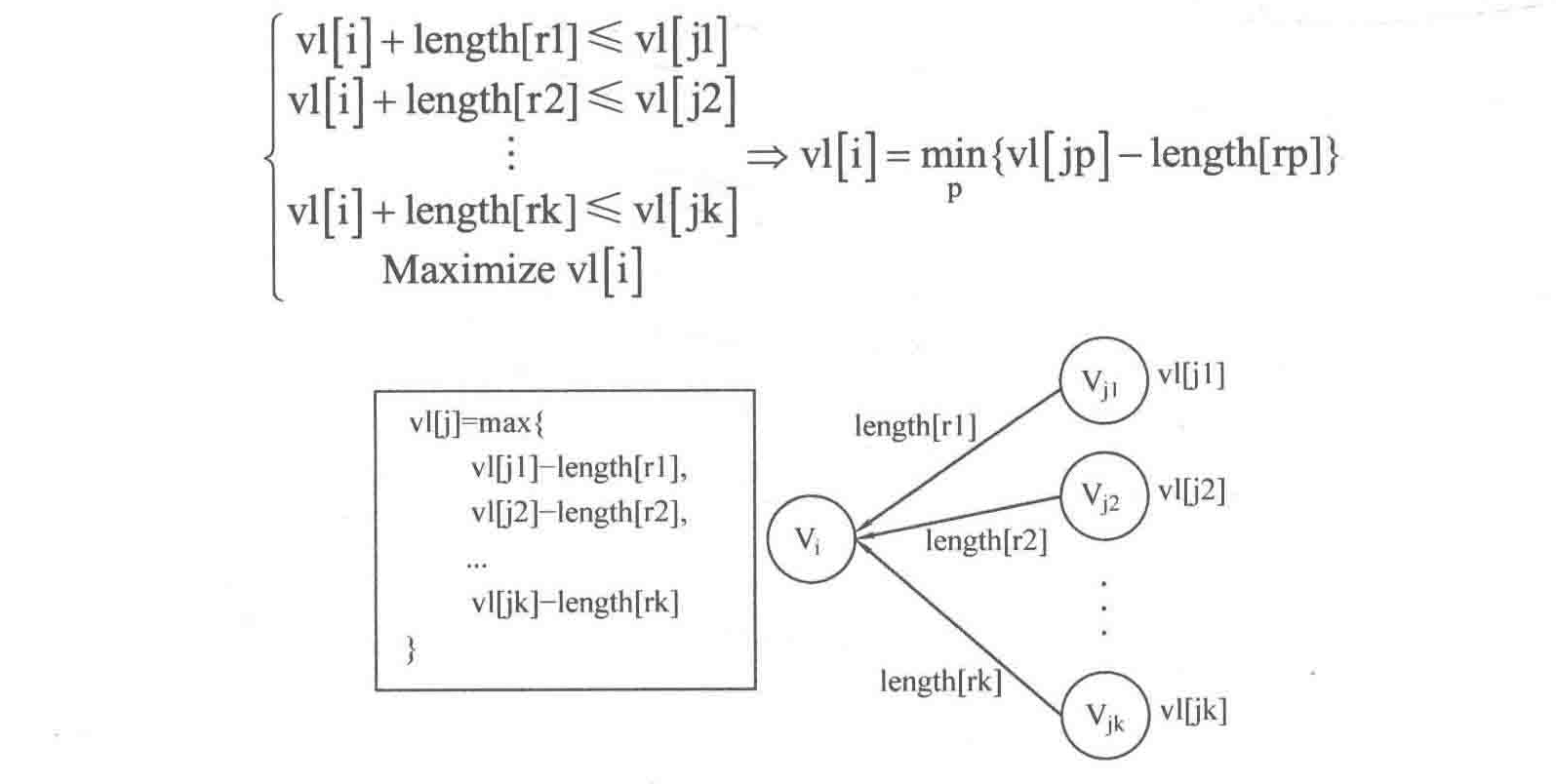
这里与ve求解不同之处在于,需要先直到后继事件的vl值,因此,使用拓扑序列的逆序来处理,这个时候,将记录了拓扑序列的栈按顺序出栈便是拓扑排序的逆序,由此从后往前推算vl数组,代码实现如下:
void get_vl(int maxlen) //拓扑排序得到的关键路径长度
fill(vl,vl+MAXV,maxlen); //初始化vl数组为关键路径的长度
while(!toporder.empty()){ //拓扑序列出栈,逆过程更新vl
int u=toporder.top();
toporder.pop();
for(int i=1;i<=n;i++){ //用u的后继结点的vl值来更新vl[u]
if(G[u][i]!=INF){
if(vl[i]-G[u][i]<vl[u]){ //vl[u]为其前驱活动开始的最小值
vl[u]=vl[i]-G[u][i];
}
}
}
}③计算每个活动的e和l
void get_path{
for(int i=0;i<m;i++){ //遍历所有的边,计算每一个活动的e和l
v[i].e=ve[v[i].st];
v[i].l=vl[v[i].ed]-v[i].len;
if(v[i].e==v[i].l){ //如果是关键路径则输出
printf("%d-%d\n",v[i].st,v[i].ed);
}
}
}可以根据情况将以上的函数进行组和或者拆分,以达到按要求输出的目的
基于动态规划的关键路径求解
有向无环图的关键路径就是DAG图中的最长路径,即整个工程的最终时间。如果只是求解最长路径,这里采用动态规划的方法解决这个问题。
可根据实际情况着重解决一下两类问题:一、求解整个图中的最长路径,即不固定起点和终点;二、固定终点,求DAG的最长路径。
对于第一个问题,采用一个数组dp,其中dp[i]表示从i号顶点出发能得到的最长路径长度,同样的,如何求得的dp[i]?这里借用求解vl数组的思路,如果对事件Vi的后继有k个事件Vj1~ Vjk分别由权值为length[r1]~length[rk]的活动边r1~rk连接,且对于后继的事件其dp已知,显然dp[i]等于dp[j1]+length[r1]~dp[jk]+length[rk]的最大值,示意图如下所示:
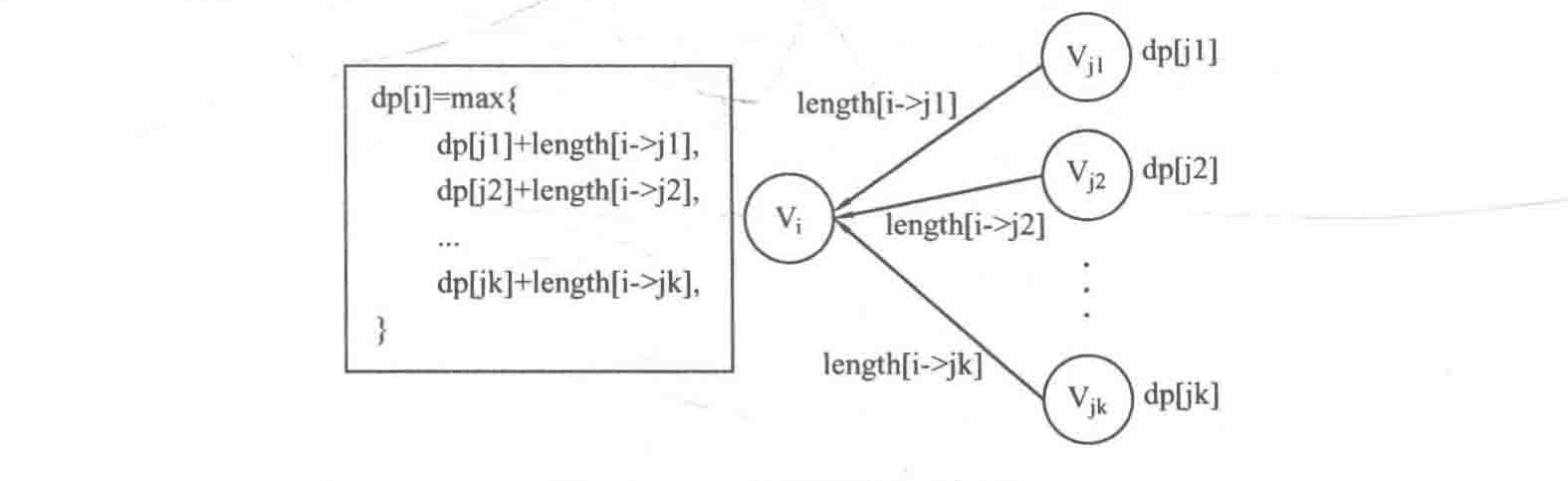
为了让算法变得简洁,可以采用递归的写法获得dp数组的求解,代码如下:
int dp[MAXV]={0}; //由于递归求解最后一层是图的汇点,从它出发的最长路径便是0,因此dp数组初始化为0,作为递归的边界
int choice[MAXV]; //记录每个结点的后继,初始化为-1
fill(choice,choice+MAXV,-1); //提前在外部,初始化路径数组
int DP(int i){
if(dp[i]>0) return dp[i]; //如果dp已经求得,直接返回结果
for(int j=0;j<n;j++){ //对i的所有后继顶点进行遍历
if(G[i][j]!=INF){ //令dp[i]等于dp[j1]+length[r1]~dp[jk]+length[rk]的最大值
int temp=DP[j]+G[i][j];
if(temp>dp[i]){ //如果更新了dp[i],则更新i在路径上的后继
dp[i]=temp;
choice[i]=j;
}
}
}
return dp[i];
}
//求个dp数组后将dp数组中的最大值(即关键路径长度)的下标i交给打印函数,用于打印路径
void Print_path(int i){
printf("%d",i); //打印路径的起始顶点
while(choice[i]!=-1){ //当不到汇点的时候进行循环
i=choice[i]; //i往后一步成为其后继
printf("->%d",i) //打印路径
}
} 以上算法,由于遍历的时候后继顶点的遍历是从编号从小到大进行的,因此实现了得到路径的字典序最小的方案。如果有更多条路径,choice数组可以改为vector二维数组,向Dijkstra+DFS一样得到多条路径,并按照要求选择。
接下来考虑,限定终点的条件下,如何求解。限定了顶点T为结束顶点时,则需要递归边界在T处停止,因此初始化,dp[T]=0,其他初始化为一个很大的负数 -INF,以表示不可到达,只能达到T,同时加入访问标记数组,使得其他顶点不会因为多次访问是的dp值变得影响dp[T],其他的代码同上类似,只不过dp数组的含义,因为初始化的限制条件,dp[i]变为了从i到达终点T的最长路径:
fill(choice,choice+MAXV,-INF); //初始化路径数组
dp[T]=0;
vis[MAXV]={false};
int DP(int i){
if(vis[i]) return dp[i]; //如果dp已经求得,直接返回结果
vis[i]=true;
for(int j=0;j<n;j++){ //对i的所有后继顶点进行遍历
if(G[i][j]!=INF){ //令dp[i]等于dp[j1]+length[r1]~dp[jk]+length[rk]的最大值
int temp=DP[j]+G[i][j];
if(temp>dp[i]){ //如果更新了dp[i],则更新i在路径上的后继
dp[i]=temp;
choice[i]=j;
}
}
}
return dp[i];
}









Comments | 2 条评论
这是一条私密评论
@HB 好的呢